题目内容
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,且OA=3,OC=2,将矩形OABC向上平移4个单位得到矩形O1A1B1C1 . 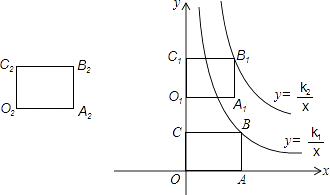
(1)若反比例函数y= ![]() 和y=
和y= ![]() 的图象分别经过点B、B1 , 求k1和k2的值;
的图象分别经过点B、B1 , 求k1和k2的值;
(2)将矩形O1A1B1C1向左平移得到O2A2B2C2 , 当点O2、B2在反比例函数y= ![]() 的图象上时,求平移的距离和k3的值.
的图象上时,求平移的距离和k3的值.
【答案】
(1)
解:∵矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,且OA=3,OC=2,
∴B(3,2),
∵反比例函数y= ![]() 的图象分别经过点B,
的图象分别经过点B,
∴k1=3×2=6;
∵将矩形OABC向上平移4个单位得到矩形O1A1B1C1,
∴B1(3,6),
∵反比例函数y= ![]() 的图象经过点B1,
的图象经过点B1,
∴k2=3×6=18;
(2)
解:设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2,则O2(﹣a,4),B2(3﹣a,6),
∵点O2、B2在反比例函数y= ![]() 的图象上,
的图象上,
∴k3=﹣4a=6(3﹣a),
解得a=9,k3=﹣36.
【解析】(1)将B(3,2)代入y= ![]() ,即可求出k1的值;将B1(3,6)代入y=
,即可求出k1的值;将B1(3,6)代入y= ![]() ,即可求出k2的值;(2)设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2 , 根据向左平移,横坐标相减,纵坐标不变得到点O2(﹣a,4),B2(3﹣a,6),由点O2、B2在反比例函数y=
,即可求出k2的值;(2)设将矩形O1A1B1C1向左平移a个单位得到O2A2B2C2 , 根据向左平移,横坐标相减,纵坐标不变得到点O2(﹣a,4),B2(3﹣a,6),由点O2、B2在反比例函数y= ![]() 的图象上,得出k3=﹣4a=6(3﹣a),解方程即可求出a与k3的值.
的图象上,得出k3=﹣4a=6(3﹣a),解方程即可求出a与k3的值.
【考点精析】本题主要考查了比例系数k的几何意义和平移的性质的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在160cm至170cm(不含170cm)的学生约有400人
其中合理的说法是( )
A.①②
B.①④
C.②④
D.③④