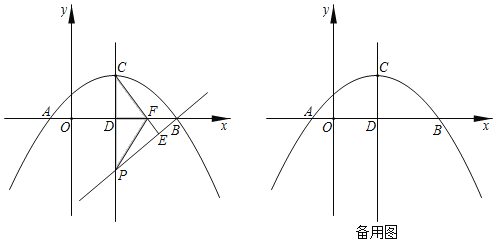
题目内容
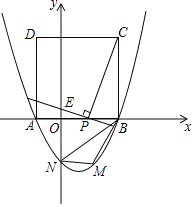
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,顶点为
两点,顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线对称轴
为抛物线对称轴![]() 上的一动点(点
上的一动点(点![]() 不与
不与![]() 重合).过点
重合).过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当
当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 当△PCF为等腰三角形时,请直接写出点
当△PCF为等腰三角形时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点 ![]() 或
或![]() .
.
【解析】
![]() 把
把![]() 代入函数,利用交点式求解即可.
代入函数,利用交点式求解即可.
![]() 先求出点C,设点
先求出点C,设点![]() 然后得函数
然后得函数![]() 的表达式为:
的表达式为:![]() ,根据
,根据![]() ,得故直线
,得故直线![]() 表达式中的
表达式中的![]() 值为
值为![]() ,求出直线
,求出直线![]() 的表达式为
的表达式为![]() ,联立①②并解得:
,联立①②并解得: ![]() ,求出
,求出![]() ,利用
,利用![]() 的面积为
的面积为![]() ,求出m即可;
,求出m即可;
![]() 由点
由点![]() 的坐标得:
的坐标得:![]() 分别算出
分别算出![]() ,
,![]() ,
,![]() 时的m即可.
时的m即可.
解:![]() 将抛物线化为交点式:
将抛物线化为交点式:![]()
将![]() 代入可得
代入可得
![]()
![]() .
.
故抛物线解析式为![]() .
.
![]() 抛物线的对称轴为
抛物线的对称轴为![]() ,则点
,则点![]()
设点![]()
将点![]() 的坐标代入一次函数表达式:
的坐标代入一次函数表达式:![]() 并解得:
并解得:
函数![]() 的表达式为:
的表达式为: ![]()
![]() 故直线
故直线![]() 表达式中的
表达式中的![]() 值为
值为![]() ,
,
将点![]() 的坐标代入一次函数表达式,
的坐标代入一次函数表达式,
同理可得直线![]() 的表达式为:
的表达式为: ![]()
联立①②并解得: ![]()
故点![]()
![]()
解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]()
![]() 由
由![]() 确定的点
确定的点![]() 的坐标得:
的坐标得:
![]()
①当![]() 时,即:
时,即: ![]() ,解得
,解得![]() :或
:或![]() (均舍去),
(均舍去),
②当![]() 时,
时, ![]() ,解得:
,解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
③当![]() 时,同理可得:
时,同理可得:![]() (舍去
(舍去![]() ),
),
故点 ![]() 或
或![]() .
.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
王方 | 7 | 10 | 9 | 8 | 6 | 9 | 9 | 7 | 10 | 10 |
李明 | 8 | 9 | 8 | 9 | 8 | 8 | 9 | 8 | 10 | 8 |
(1)根据以上数据,将下面两个表格补充完整:
王方10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 | |
频数 | ______ | ______ | ______ | ______ | ______ | |
频率 | ______ | ______ | ______ | ______ | ______ |
李明10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 |
频数 | ______ | ______ | ______ | ______ | ______ |
频率 | ______ | ______ | ______ | ______ | ______ |
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,应选派谁参加比赛合适.