��Ŀ����
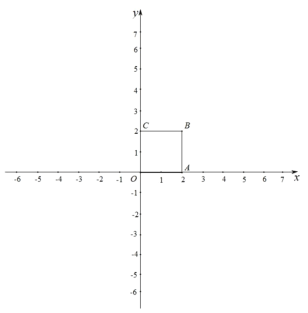
����Ŀ����ͼ1��ƽ������һ��![]() ��
��![]() ����������ľ���ֱ�Ϊ
����������ľ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ������
������![]() ����Ƶ�
����Ƶ�![]() Ϊ
Ϊ![]() ���ڵ�
���ڵ�![]() �Ĺ��ɵ㣮
�Ĺ��ɵ㣮
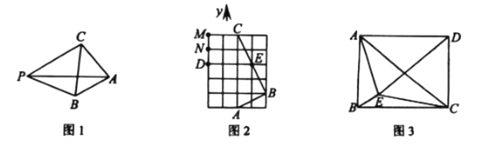
��1����ͼ2����![]() �������У�ÿ��С�����εı߳���Ϊ1����
�������У�ÿ��С�����εı߳���Ϊ1����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����С�����εĶ����ϣ����E��
����С�����εĶ����ϣ����E��![]() ���ڵ�B�Ĺ��ɵ�.
���ڵ�B�Ĺ��ɵ�.
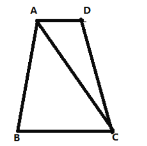
��2����ͼ3��![]() �Ǿ���
�Ǿ���![]() ��һ�㣬�ҵ�
��һ�㣬�ҵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() �Ĺ��ɵ�,
�Ĺ��ɵ�,
����֤��![]() ��
��
����![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
��3����ͼ3������![]() �У�
��![]() ��
��![]() ��
��![]() �Ǿ���
�Ǿ���![]() ��һ�㣬�ҵ�
��һ�㣬�ҵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() �Ĺ��ɵ㣮
�Ĺ��ɵ㣮
�ٵ�![]() ʱ����
ʱ����![]() �ij���
�ij���
��ֱ��д��![]() ����Сֵ��
����Сֵ��
���𰸡���2����֤������������30������3����AE�ij�Ϊ![]() ��
��![]() ����
����![]() ��
��
��������
��2�����ɾ������ʵá�ADC=90�����ɵ�AD2+DC2=AC2�����ݹ�������BC2+EC2=AC2������ΪAD=BC������CE=CD��
�����CED=�������ݡ�AEC=135����CE=CD����ADC=90������������ʾ��ADE�������ڽǣ������������ڽǺ�180��Ϊ������ϵ�з��̣�����������������ADE��
��3������������C����ABE���ڵ�A�Ĺ��ɵ����Կɵ�CE=CD=5����Ϊ����ʹ�ã��١�ADE�ǵ������������3��������ۣ���ÿ�������ͼ�ٸ��ݾ������ʺ��ɶ������㣬������AE�ij�������CB�Ͻ�ȡCH=![]() ���������߶�Ӧ�ɱ������н���ȹ�����ECH�ס�BCE����
���������߶�Ӧ�ɱ������н���ȹ�����ECH�ס�BCE����![]() BEת��ΪEH�����Ե���A��E��H��ͬһֱ����ʱ��AE+
BEת��ΪEH�����Ե���A��E��H��ͬһֱ����ʱ��AE+![]() BE=AHȡ����Сֵ�����ù��ɶ������AH���ɣ�
BE=AHȡ����Сֵ�����ù��ɶ������AH���ɣ�
�⣺��2����֤�����ߵ�C����ABE���ڵ�A�Ĺ��ɵ�
��CA2=CB2+CE2
���ı���ABCD�Ǿ���
��AB=CD��AD=BC����ADC=90��
��CA2=AD2+CD2=CB2+CD2
��CB2+CE2=CB2+CD2
��CE=CD
�����CED=�������CDE=��CED=��
���ADE=��ADC-��CDE=90��-��
�ߡ�AEC=135��
���AED=��AEC-��CED=135��-��
��DA=DE
���DAE=��DEA=135��-��
�ߡ�DAE+��DEA+��ADE=180��
��2��135��-����+��90��-����=180��
����=60��
���ADE=90��-60��=30��
��3���١߾���ABCD�У�AB=5��BC=8
��AD=BC=8��CD=AB=5
�ߵ�C����ABE���ڵ�A�Ĺ��ɵ�
��CE=CD=5
i����ͼ1����DE=DA����DE=8
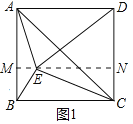
����E��MN��AB�ڵ�M����DC�ڵ�N
���AME=��MND=90��
���ı���AMND�Ǿ���
��MN=AD=8��AM=DN
��AM=DN=x����CN=CD-DN=5-x
��Rt��DEN��EN2+DN2=DE2��Rt��CEN��EN2+CN2=CE2
��DE2-DN2=CE2-CN2
��82-x2=52-��5-x��2
��ã�x=![]()
��EN=![]() ��AM=DN=
��AM=DN=![]()
��ME=MN-EN=8-![]() ,
,
��Rt��AME��AE=![]()
ii����ͼ2����AE=DE����E��AD�Ĵ�ֱƽ������
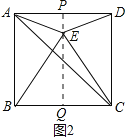
����E��PQ��AD�ڵ�P����BC�ڵ�Q
��AP=DP=![]() AD=4����APQ=��PQC=90��
AD=4����APQ=��PQC=90��
���ı���CDPQ�Ǿ���
��PQ=CD=5��CQ=PD=4
��Rt��CQE��EQ=![]() ��3
��3
��PE=PQ-EQ=2
��Rt��APE��AE=![]()
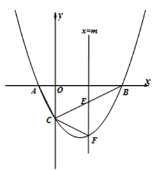
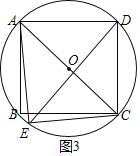
iii����ͼ3����AE=AD=8����AE2+CE2=AD2+CD2=AC2
���AEC=90��
ȡAC�е�O�����A��B��C��D����OΪԲ�ġ�OAΪ�뾶�ġ�O��
���EҲ�ڡ�O��
���E���ھ���ABCD�ڲ�������������
��������������ADE�ǵ��������Σ�AE�ij�Ϊ![]() ��
��![]() ��
��
����CB�Ͻ�ȡCH=![]() ������EH
������EH
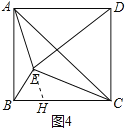
��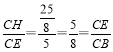 ,
,
�ߡ�ECH=��BCE
���ECH�ס�BCE
��![]() ,
,
��EH=![]() BE
BE
��AE+![]() BE=AE+EH
BE=AE+EH
�൱��A��E��H��ͬһֱ����ʱ��AE+![]() BE=AHȡ����Сֵ
BE=AHȡ����Сֵ
��BH=BC-CH=8-![]() ��
��![]() ,
,
��AH=![]()
��AE+![]() BE����СֵΪ
BE����СֵΪ![]() ��
��