题目内容
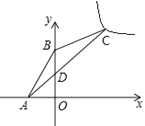
【题目】如图,在平面直角坐标系![]() 中,点A(
中,点A(![]() ,0),B(0,2),点C在第一象限,∠ABC=135°,AC交
,0),B(0,2),点C在第一象限,∠ABC=135°,AC交![]() 轴于D,CD=3AD,反比例函数
轴于D,CD=3AD,反比例函数![]() 的图象经过点C,则
的图象经过点C,则![]() 的值为_______.
的值为_______.
【答案】9
【解析】
过点A作AH⊥CB的延长线于点H,得到AH=BH=![]() =
=![]() ,根据已知条件得到B,H,A,O四点共圆,连接OH,推出H在第二象限角平分线上,作HM⊥x轴于M,HN⊥y轴于N,根据全等三角形的性质得到AM=BN=
,根据已知条件得到B,H,A,O四点共圆,连接OH,推出H在第二象限角平分线上,作HM⊥x轴于M,HN⊥y轴于N,根据全等三角形的性质得到AM=BN=![]() ,求得直线HB的解析式,于是得到结论.
,求得直线HB的解析式,于是得到结论.
解:∵点A(![]() ,0),B(0,2),
,0),B(0,2),
∴OA=1,OB=2,
∴![]() ;
;
如图,过点A作AH⊥CB的延长线于点H,
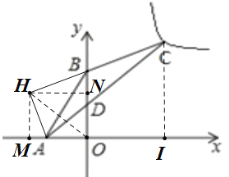
∵∠ABC=135°,
∴∠HBA=HAB=45°,
∴AH=BH=![]() =
=![]() ,
,
∵BH⊥AH,BO⊥AO,
∴B,H,A,O四点共圆,
连接OH,则∠BOH=∠BAH=45°,
∴H在第二象限角平分线上,
作HM⊥x轴于M,HN⊥y轴于N,
则四边形HMON是正方形,
∴HM=HN,
∵AH=BH,
∴Rt△HAM≌Rt△HBN,
∴AM=BN,
∵OM=ON,
∴AM=BN=![]() ,
,
∴H(![]() ,
,![]() ),
),
∴直线BH的解析式为y=![]() x+2,
x+2,
过C作CI⊥x轴于I,
∴OD∥CI,
∴![]() ,
,
∴OI=3AO=3,
把x=3代入y=![]() x+2得y=3,
x+2得y=3,
∴C点坐标为(3,3).
∵点C在反比例函数![]() 的图像上,
的图像上,
∴![]() ;
;
故答案为:9.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目