题目内容
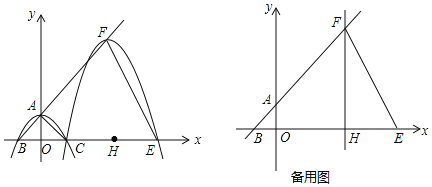
【题目】如图1,已知抛物线y=![]() x2+bx+c经过点A(3,0),点B(﹣1,0),与y轴负半轴交于点C,连接BC、AC.
x2+bx+c经过点A(3,0),点B(﹣1,0),与y轴负半轴交于点C,连接BC、AC.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得以A、B、C、P为顶点的四边形的面积等于△ABC的面积的![]() 倍?若存在,求出点P的坐标;若不存在,请说明理由.
倍?若存在,求出点P的坐标;若不存在,请说明理由.
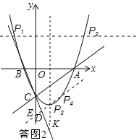
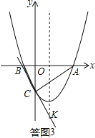
(3)如图2,直线BC与抛物线的对称轴交于点K,将直线AC绕点C按顺时针方向旋转α°,直线AC在旋转过程中的对应直线A′C与抛物线的另一个交点为M.求在旋转过程中△MCK为等腰三角形时点M的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;(2)存在符合条件的点P,且坐标为(
;(2)存在符合条件的点P,且坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、(1,﹣
)、(1,﹣![]() )、(2,﹣
)、(2,﹣![]() );(3)点M的坐标是(2,﹣
);(3)点M的坐标是(2,﹣![]() )或(1,﹣
)或(1,﹣![]() ).
).
【解析】
(1)知道A、B两点坐标后,利用待定系数法可确定该抛物线的解析式.(2)此题中,以A、B、C、P为顶点的四边形可分作两部分,若该四边形的面积是△ABC面积的1.5倍,那么四边形中除△ABC以外部分的面积应是△ABC面积的一半,分三种情况:①当点P在x轴上方时,△ABP的面积应该是△ABC面积的一半,因此点P的纵坐标应该是点C纵坐标绝对值的一半,代入抛物线解析式中即可确定点P的坐标;②当点P在B、C段时,显然△BPC的面积要远小于△ABC面积的一半,此种情况不予考虑;③当点P在A、C段时,由A、C的长以及△ACP的面积可求出点P到直线AC的距离,首先在射线CK上取线段CD,使得CD的长等于点P到直线AC的距离,先求出过点D且平行于l1的直线解析式,这条直线与抛物线的交点即为符合条件的点P.(3)从题干的旋转条件来看,直线l1旋转的范围应该是直线AC、直线BC中间的部分,而△MCK的腰和底并不明确,所以分情况讨论:①CK=CM、②KC=KM、③MC=MK;求出点M的坐标.
解:(1)如图1,
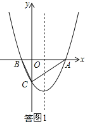
∵点A(3,0),点B(﹣1,0),
∴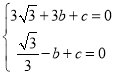 ,解得
,解得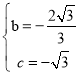 ,
,
则该抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;
;
(2)易知OA=3、OB=1、OC=![]() ,则:S△ABC=
,则:S△ABC=![]() ABOC=
ABOC=![]() ×4×
×4×![]() =2
=2![]() .
.
①当点P在x轴上方时,由题意知:S△ABP=![]() S△ABC,则:
S△ABC,则:
点P到x轴的距离等于点C到x轴距离的一半,即 点P的纵坐标为![]() ;
;
令y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() =
=![]() ,化简得:2x2﹣4x﹣9=0
,化简得:2x2﹣4x﹣9=0
解得 x=![]() ;
;
∴P1(![]() ,
,![]() )、P2(
)、P2(![]() ,
,![]() );
);
②当点P在抛物线的B、C段时,显然△BCP的面积要小于![]() S△ABC,此种情况不合题意;
S△ABC,此种情况不合题意;
③当点P在抛物线的A、C段时,S△ACP=![]() ACh=
ACh=![]() S△ABC=
S△ABC=![]() ,则h=1;
,则h=1;
在射线CK上取点D,使得CD=h=1,过点D作直线DE∥AC,交y轴于点E,
如图2;
在Rt△CDE中,∠ECD=∠BCO=30°,CD=1,则CE=![]() 、OE=OC+CE=
、OE=OC+CE=![]() ,点E(0,﹣
,点E(0,﹣![]() )
)
∴直线DE:y=![]() x﹣
x﹣![]() ,联立抛物线的解析式,有:
,联立抛物线的解析式,有: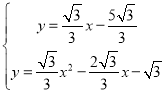 ,
,
解得: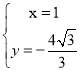 或
或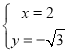 ,
,
∴P3(1,-![]() )、P4(2,-
)、P4(2,-![]() );
);
综上,存在符合条件的点P,坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(1,-
),(1,-![]() ),(2,-
),(2,-![]() );
);
(3)如图3,
由(1)知:y=![]() x2-
x2-![]() x-
x-![]() =
=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
∴抛物线的对称轴 x=1;
①当KC=KM时,点C、M1关于抛物线的对称轴x=1对称,则点M1的坐标是(2,﹣![]() );
);
②KC=CM时,K(1,﹣2![]() ),KC=BC.则直线A′C与抛物线的另一交点M2与点B重合,M、C、K三点共线,不能构成三角形;
),KC=BC.则直线A′C与抛物线的另一交点M2与点B重合,M、C、K三点共线,不能构成三角形;
③当MK=MC时,点D是CK的中点.
∵∠OCA=60°,∠BCO=30°,
∴∠BCA=90°,即BC⊥AC,则作线段KC的中垂线必平行AC且过点D,
∴点M3与点P3(1,-![]() )、P4(2,-
)、P4(2,-![]() )重合,
)重合,
综上所述,点M的坐标是(2,﹣![]() )或(1,﹣
)或(1,﹣![]() ).
).

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.
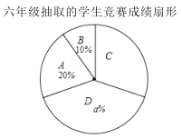
【题目】面对疫情,每个人都需要积极行动起来,做好预防工作.为此某校开展了“新型冠状病毒肺炎”防控知识竞赛.现从该校五、六年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:A.
表示,共分成四组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
五年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
六年级10名学生的竞赛成绩在C组中的数据是:94,90,94
五、六年级抽取的学生竞赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
五年级 | 92 | 93 |
| 52 |
六年级 | 92 |
| 100 | 50.4 |
是据以上信息,解答下列问题:
(1)直接写出上述图表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上数据,你认为该校五、六年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校五、六年级共1800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀![]() 的学生人数是多少?
的学生人数是多少?
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.