题目内容
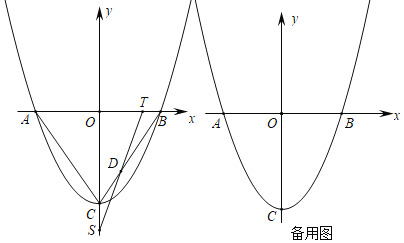
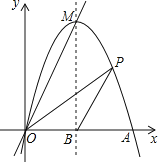
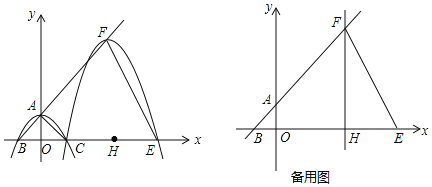
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B、C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
(1)求a、c的值;
(2)连接OF,求△OEF的周长;
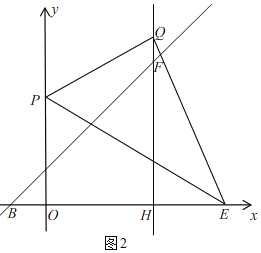
(3)现将一足够大的三角板的直角顶点Q放在射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使得以点P、Q、E为顶点的三角形与△POE全等?若存在,请直接写出Q点坐标;若不存在,请说明理由.
【答案】(1)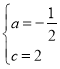 ;(2)20+4
;(2)20+4![]() ;(3)存在,点Q(6,2
;(3)存在,点Q(6,2![]() )或Q(6,3).
)或Q(6,3).
【解析】
(1)根据直角三角形的性质,可得B(﹣2,0),A(0,2),C(2,0),将点代入解析式即可求a,c的值;
(2)求出AB的直线解析为y=x+2,设F(m,m+2),平移后抛物线解析式y=﹣![]() (x﹣m)2+m+2,将点C(2,0)代入,得平移后抛物线解析式为y=﹣
(x﹣m)2+m+2,将点C(2,0)代入,得平移后抛物线解析式为y=﹣![]() x2+6x﹣10,进而求出点E的坐标,即可得出结论;
x2+6x﹣10,进而求出点E的坐标,即可得出结论;
(3)当P在x轴上方时,由△PQE≌△POE,可得QE=OE=10,在Rt△QHE中,OH=![]() =2
=2![]() ,则Q(6,2
,则Q(6,2![]() );当P在x轴下方时,PQ=OE=10,过点P作PK⊥HF与点K,可证明△PKQ∽△QHE,则
);当P在x轴下方时,PQ=OE=10,过点P作PK⊥HF与点K,可证明△PKQ∽△QHE,则![]() ,则Q(6,3),即可得出结论.
,则Q(6,3),即可得出结论.
解:(1)∵△ABC为等腰直角三角形,
∴AO=![]() BC,
BC,
∵△ABC面积为4,
∴![]() BCOA=4,
BCOA=4,
∴OA=2,BO=4,
∴B(﹣2,0),A(0,2),C(2,0),
∵点A,B在抛物线y=ax2+c上,
∴![]() ,
,
∴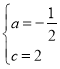 ,
,
即a、c的值分别为﹣![]() 和2;
和2;
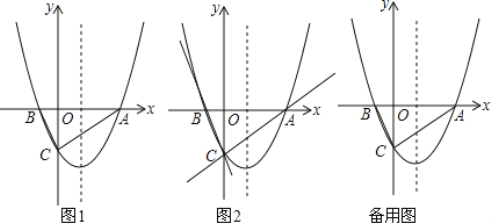
(2)如图1,连接OF,
由(1)可知:y=﹣![]() x2+2,
x2+2,
∵B(﹣2,0),A(/span>0,2),
∴AB的直线解析为y=x+2,
∵平移后抛物线顶点F在射线BA上,
设F(m,m+2),
∴平移后抛物线解析式y=﹣![]() (x﹣m)2+m+2,
(x﹣m)2+m+2,
将点C(2,0)代入y=﹣![]() (x﹣m)2+m+2,得
(x﹣m)2+m+2,得
﹣![]() (2﹣m)2+m+2=0,
(2﹣m)2+m+2=0,
∴m=6或m=0(舍),
∴F(6,8),
∴平移后抛物线解析式为y=﹣![]() x2+6x﹣10,
x2+6x﹣10,
当y=0时,﹣![]() x2+6x﹣10=0,
x2+6x﹣10=0,
∴x=2或x=10,
∴E(10,0),
∴OE=10,
∵F(6,8),
∴OF=![]() =10,EF=
=10,EF=![]() =4
=4![]() ,
,
∴△OEF的周长为OE+OF+EF=10+10+4![]() =20+4
=20+4![]() ;
;
(3)当P在x轴上方时,如图2,
∵△PQE≌△POE,
∴QE=OE=10,
在Rt△QHE中,HQ=![]() =2
=2![]() ,
,
∴Q(6,2![]() ),
),
当P在x轴下方时,如图3,
∵△PQE≌△EOP,
∴PQ=OE=10,
过点P作PK⊥HF与点K,
∴PK=6,
在Rt△PQK中,QK=![]() =8,
=8,
∵∠PQE=90°,
∴∠PQK+∠HQE=90°,
∵∠HQE+∠HEQ=90°,
∴∠PQK=∠HEQ,
∵∠PKQ=∠QHE=90°,
∴△PKQ∽△QHE,
∴![]() ,
,
∴![]() ,
,
∴QH=3,
∴Q(6,3),
综上所述:满足条件的点Q(6,2![]() )或Q(6,3).
)或Q(6,3).



【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3