题目内容
【题目】如图,正方形ABCD中,点E是BC边上的一个动点,连接AE,将线段AE绕点A逆时针旋转90°,得到AF,连接EF,交对角线BD于点G,连接AG.
(1)根据题意补全图形;
(2)判定AG与EF的位置关系并证明;
(3)当AB=3,BE=2时,求线段BG的长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据题意补全图形即可;
(2)先判断出△ADF≌△ABE,进而判断出点C,D,F共线,即可判断出△DFG≌△HEG,得出FG=EG,即可得出结论;
(3)先求出正方形的对角线BD,再求出BH,进而求出DH,即可得出HG,求和即可得出结论.
(1)补全图形如图所示,
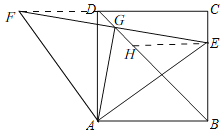
(2)连接DF,
由旋转知,AE=AF,∠EAF=90°,
∵四边形ABCD是正方形,
∴AB∥CD,AD=AB,∠ABC=∠ADC=BAD=90°,
∴∠DAF=∠BAE,
∴△ADF≌△ABE(SAS),
∴DF=BE,∠ADF=∠ABC=90°,
∴∠ADF+∠ADC=180°,
∴点C,D,F共线,
∴CF∥AB,
过点E作EH∥BC交BD于H,
∴∠BEH=∠BCD=90°,DF∥EH,
∴∠DFG=∠HEG,
∵BD是正方形ABCD的对角线,
∴∠CBD=45°,
∴BE=EH,
∵∠DGF=∠HGE,
∴△DFG≌△HEG(AAS),
∴FG=EG
∵AE=AF,
∴AG⊥EF;
(3)∵BD是正方形的对角线,
∴BD=![]() AB=3
AB=3![]() ,
,
由(2)知,在Rt△BEH中,BH=![]() BE=2
BE=2![]() ,
,
∴DG=BD-BH=![]()
由(2)知,△DFG≌△HEG,
∴DG=HG,
∴HG=![]() DH=
DH=![]() ,
,
∴BG=BH+HG=2![]() +
+![]() =
=![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目







