题目内容
如图,四边形ABCD的对角线AC和BD相交于O点,如果S△ABD=5,S△ABC=6,S△BCD=10,那么S△OBC .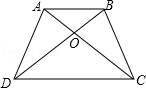

4
试题分析:先设出一个三角形的面积:△AOB的面积是s1=x,再用代数式表示出图中其它三角形的面积,利用中间桥
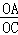 得出方程,进一步求出结果.
得出方程,进一步求出结果.解:设△AOB的面积是s1=x,则△ADO的面积是ss2=5﹣x,△BOC的面积是s3=6﹣x,△DOC的面积是s4=10﹣(6﹣x)=4+x,
∵△ABO的边OA上和△BOC的边上的高相等,
∴
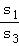 =
= ,
,同理
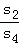 =
= ,
,∴
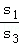 =
=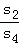 ,
,即
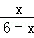 =
= ,
,解得:x=2,
∴S△OBC=6﹣2=4.
点评:解此题的关键是灵活运用三角形的面积公式,等高时面积比等于边之比,从而转化成解方程,求出未知数的值.

练习册系列答案
相关题目
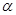 等于( )
等于( )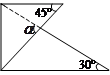

 是△ABC的重心,若
是△ABC的重心,若 ,则
,则 .
.