Question

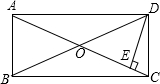
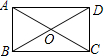
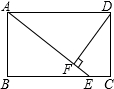
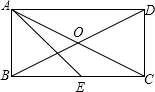
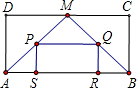
如图，在矩形ABCD中，M为CD的中点，连接AM、BM，分别取AM、BM的中点P、Q，以P、Q为顶点作第二个矩形PSRQ，使S、R在AB上．在矩形PSRQ中，重复以上的步骤继续画图…．若AM⊥MB，矩形ABCD的周长为30．则：
（1）DC=______；（2）第n个矩形的边长分别是______．

Answer 1

（1）∵AM⊥MB，且M为CD的中点，AM=MB，
∴∠DAM=∠DMA，∴AD=DM=

1

2

CD，
又已知矩形ABCD的周长为30，所以CD=10，
故答案为10，

（2）由第一问求得：第一个矩形的长为：10，宽为5，
又点P、Q是AM、BM的中点，所以之后得到的矩形长宽比例为2：1，
在△ABM中，PQ=5，则宽为

5

2

，
则可得出：第n个矩形的边长分别是10×(

1

2

)n-1，5×(

1

2

)n-1，
故答案为10×(

1

2

)n-1，5×(

1

2

)n-1，