题目内容
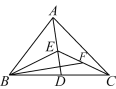
【题目】如图,在△ABC中,D,E,F分别是BC,AD,CE边上的中点,且S△ABC=16 cm2,则S△BEF=_________.
【答案】4cm2
【解析】
根据等底等高的三角形的面积相等用△ABC的面积表示出△BDE和△CDE的面积,从而得到△BCE的面积,再次利用等底等高的三角形的面积相等即可得到△BEF的面积与△ABC的面积的关系,然后代入数据进行计算即可得解.
∵点D,E分别是BC,AD边上的中点,
∴S△ABD=S△ACD=![]() S△ABC,
S△ABC,
S△BDE=![]() S△ABD=
S△ABD=![]() S△ABC,
S△ABC,
S△CDE=![]() S△ACD=
S△ACD=![]() S△ABC,
S△ABC,
∴S△BCE=S△BDE+S△CDE=![]() S△ABC+
S△ABC+![]() S△ABC=
S△ABC=![]() S△ABC,
S△ABC,
∵F是CE边上的中点,
∴S△BEF=![]() S△BCE=
S△BCE=![]() ×
×![]() S△ABC=
S△ABC=![]() S△ABC,
S△ABC,
∵S△ABC=16cm2,
∴S△BEF=![]() ×16=4cm2.
×16=4cm2.
故答案为:4cm2.

练习册系列答案
相关题目





