题目内容
【题目】折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC,若∠A=75°,∠C=60°,则∠BDF=____________________________
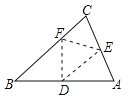
【答案】90°
【解析】分析: 根据三角形的内角和定理求出∠B,再根据两直线平行,同位角相等∠ADE,根据翻折变换的性质可得∠EDF=∠ADE,然后根据平角的定义列式计算即可得解.
详解: :∵∠A=75°,∠C=60°,
∴∠B=180°-∠A-∠C=180°-75°-60°=45°,
∵DE∥BC,
∴∠ADE=∠B=45°,
由翻折的性质得,∠EDF=∠ADE=45°,
∴∠BDF=180°-45°×2=90°.
故答案为:90°.
点睛: 本题考查了三角形的内角和定理,平行线的性质,翻折变换的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目