Question

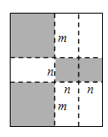
【题目】如图，将一张矩形大铁皮切割成九块，切痕如下图虚线所示，其中有两块是边长都为的大正方形，两块是边长都为的小正方形，五块是长宽分别是、的全等小矩形，且．

(1)用含的代数式表示切痕的总长为 ;

(2)若每块小矩形的面积为，四个正方形的面积和为，试求该矩形大铁皮的周长．

Answer 1

【答案】（1）；（2）84

【解析】

（1）根据切痕长有两横两纵列出算式，再根据合并同类项法则整理即可；

（2）根据小矩形的面积和正方形的面积列出算式，再利用完全平方公式整理求出m+n的值，然后根据矩形的周长公式整理求解即可．

解：（1）切痕总长=2[（m+2n）+（2m+n）]，

=2（m+2n+2m+n），

=6m+6n；

故答案为：6m+6n；

（2）由题意得：mn=48，2m2+2n2=200，

∴m2+n2=100，

∴（m+n）2=m2+n2+2mn=196，

∵m+n＞0，

∴m+n=14，

∴周长=2（m+2n+2m+n）=6m+6n=6（m+n）=84（cm）．