Question

【题目】已知，如图，在四边形ABCD中， ，延长BC至点E，连接AE交CD于点F，使

求证： ；

求证： ；

若BF平分，请写出与的数量关系______不需证明

Answer 1

【答案】（1）见解析；（2）见解析；（3）2∠AFB+∠CAF=180°

【解析】试题分析：（1）根据∠BAC=∠DAE，运用等式性质即可得出∠BAC+∠CAF=∠DAE+∠CAF，进而得到∠BAF=∠CAD；

（2）根据∠BAC=∠DAF，∠ACB=∠CFE=∠AFD，可得∠B=∠D，最后根据∠B+∠BCD=180°，可得∠D+∠BCD=180°，进而判定AD∥BE；

（3）根据AD∥BE，可得∠E=∠1=∠2，再根据BF平分∠ABC，可得∠3=∠4，根据∠AFB是△BEF的外角，得出∠AFB=∠4+∠E=∠4+∠1，即∠AFB=3+∠2，最后根据AD∥BC，得到∠ABC+∠BAD=180°，进而得到2∠AFB+∠CAF=180°．

试题解析：(1)∵∠BAC=∠DAE，

∴∠BAC+∠CAF=∠DAE+∠CAF，

∴∠BAF=∠CAD；

(2)∵∠BAC=∠DAF，∠ACB=∠CFE=∠AFD，

∴∠B=∠D，

∵AB∥CD，

∴∠B+∠BCD=180°，

∴∠D+∠BCD=180°，

∴AD∥BE；

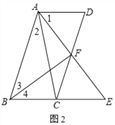
(3)如图2,∵AD∥BE,

∴∠E=∠1=∠2，

∵BF平分∠ABC，

∴∠3=∠4，

∵∠AFB是△BEF的外角，

∴∠AFB=∠4+∠E=∠4+∠1，

∴∠AFB=3+∠2，

又∵AD∥BC，

∴∠ABC+∠BAD=180°，

∴∠3+∠4+∠1+∠CAF+∠2=180°，

即2∠AFB+∠CAF=180°.

故答案为：2∠AFB+∠CAF=180°.