题目内容
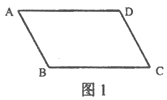
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作射线EF,
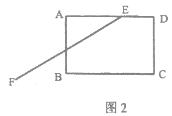
(1)若∠DAB=60°,EF∥AB交BC于点H,请在图1中补全图形,并直接写出四边形ABHE的形状;
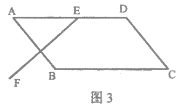
(2)如图2,若∠DAB=90°,EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG.请在图2中补全图形,并证明点A,E,B,G在同一个圆上;
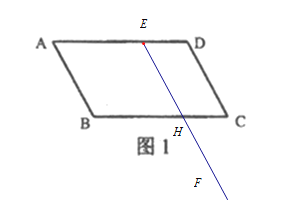
(3)如图3,若∠DAB=![]() (0°<
(0°<![]() <90°),EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG.请在图3中补全图形(要求:尺规作图,保留作图痕迹),并求出线段EG、AG、BG之间的数量关系(用含
<90°),EF与AB相交,在EF上取一点G,使得∠EGB=∠EAB,连接AG.请在图3中补全图形(要求:尺规作图,保留作图痕迹),并求出线段EG、AG、BG之间的数量关系(用含![]() 的式子表示);
的式子表示);
【答案】(1)菱形;(2)证明见解析;(3)EG=2AG·sin![]() +BG.
+BG.
【解析】
(1)根据题目要求画出示意图,根据有一组对边相等是平行四边形是菱形即可判断四边形ABHE的形状.
(2) 连接BE,OG,以BE的中点O为圆心,以OB的长为半径作圆.则![]()
根据直角三角形斜边的中线等于斜边的一半,得到![]() 根据等量代换得到
根据等量代换得到![]() 即可证明.
即可证明.
(3) 首先作∠GAH=∠EAB交GE于点H.作AM⊥EG于点M,易证得△ABG≌△AEH,又由∠EAB=α,易得![]() 继而证得结论;
继而证得结论;
(1)如图所示:
四边形ABHE为菱形.
(2)连接BE,OG,以BE的中点O为圆心,以OB的长为半径作圆.则圆O为![]() 的外接圆.
的外接圆.![]()
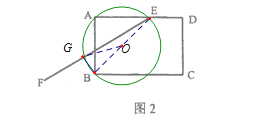
![]()
则![]()
即![]()
点A,E,B,G在同一个圆上;
(3)如图,作∠GAH=∠EAB交GE于点H.作AM⊥EG于点M,
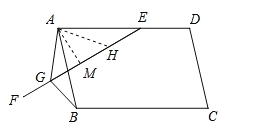
∴∠GAB=∠HAE.
∵点A,E,B,G在同一个圆上,
∴∠ABG=∠AEH.
在△ABG和△AEH中,
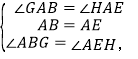
∴△ABG≌△AEH(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=α,
∴![]()
∵![]()
∴EG=GH+BG.
∴![]()

练习册系列答案
相关题目