题目内容
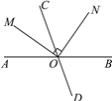
【题目】如图，点O为直线AB上一点，过点O作射线OC，使∠BOC=135°，将一个含45°角的直角三角尺的一个顶点放在点O处，斜边OM与直线AB重合，另外两条直角边都在直线AB的下方．
（1）将图1中的三角尺绕着点O逆时针旋转90°，如图2所示，此时∠BOM=_____；在图2中，OM是否平分∠CON？请说明理由；
（2）紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示，使得ON在∠AOC的内部，请探究：∠AOM与∠CON之间的数量关系，并说明理由；
（3）将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为_____（直接写出结果）．
【答案】 90°OM平分∠CON ∠AOM=∠CON (3) 4.5秒或40.5秒
【解析】试题分析：（1）根据旋转的性质可得， 
求出
的度数，即可判定OM是否平分∠CON．
根据
即可判定它们的关系.
直接写出即可.
试题解析：（1）如图2， 
OM平分∠CON．理由如下：
而
故答案为90°；
（2）
理由如下：如图3，
（3）
（秒）或
（秒）．
故答案为：4.5秒或40.5秒．
练习册系列答案
相关题目
