题目内容
如图△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB
（1）求证：四边形EFCD是菱形；
（2）设CD=4，求D、F两点间的距离．
（1）求证：四边形EFCD是菱形；
（2）设CD=4，求D、F两点间的距离．
（1）证明：∵ △ABC与△CDE都是等边三角形，
∴ ED=CD
∴ ∠A=∠DCE=∠BCA=∠DCE=60°
∴ AB∥CD，DE∥CF
又∵ EF∥AB ∴EF∥CD
∴ 四边形EFCD是菱形
（2）解：连结DF，与CE相交于点G
由CD=4，可知CG=2
∴ DG=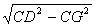
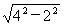
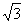
∴ DF=4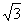
答：D、F两点间的距离为4
∴ ED=CD
∴ ∠A=∠DCE=∠BCA=∠DCE=60°
∴ AB∥CD，DE∥CF
又∵ EF∥AB ∴EF∥CD
∴ 四边形EFCD是菱形
（2）解：连结DF，与CE相交于点G
由CD=4，可知CG=2
∴ DG=
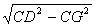
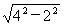
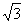
∴ DF=4
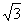
答：D、F两点间的距离为4
练习册系列答案
相关题目
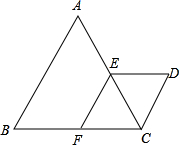如图△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB
