题目内容
如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB(1)求证:四边形EFCD是菱形;
(2)设CD=4,求D、F两点间的距离.

【答案】分析:(1)根据菱形的判定定理,一组邻边相等的平行四边形是菱形,由△ABC与△CDE都是等边三角形,可得出角之间的等量关系,从而证明四边形EFCD是菱形;
(2)连接DF,与CE相交于点G,由(1)知DF就是菱形EFCD的一条对角线,根据菱形的性质及30°特殊角的值可计算出结果.
解答:(1)证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD.
∴∠A=∠DCE=∠BCA=∠DEC=60°.(1分)
∴AB∥CD,DE∥CF.(2分)
又∵EF∥AB,
∴EF∥CD,(3分)
∴四边形EFCD是菱形.(4分)
(2)解:连接DF,与CE相交于点G,(5分)
由CD=4,可知CG=2,(6分)
∴ ,(7分)
,(7分)
∴ .(8分)
.(8分)
点评:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.
(2)连接DF,与CE相交于点G,由(1)知DF就是菱形EFCD的一条对角线,根据菱形的性质及30°特殊角的值可计算出结果.
解答:(1)证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD.
∴∠A=∠DCE=∠BCA=∠DEC=60°.(1分)
∴AB∥CD,DE∥CF.(2分)
又∵EF∥AB,
∴EF∥CD,(3分)
∴四边形EFCD是菱形.(4分)
(2)解:连接DF,与CE相交于点G,(5分)
由CD=4,可知CG=2,(6分)
∴
 ,(7分)
,(7分)∴
 .(8分)
.(8分)点评:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
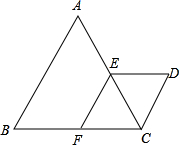 如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB
如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB

