题目内容
如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB。

(1)求证:四边形EFCD是菱形;
(2)设CD=4,求D、F两点间的距离。
(2)设CD=4,求D、F两点间的距离。
解:(1)证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD,
∴∠A=∠DCE=∠BCA=∠DEC=60°,
∴AB∥CD,DE∥CF,
又∵EF∥AB,
∴EF∥CD,
∴四边形EFCD是菱形;
(2)连接DF,与CE相交于点G,
由CD=4,可知CG=2,
∴DG= ,
,
∴DF=4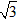 。
。
∴ED=CD,
∴∠A=∠DCE=∠BCA=∠DEC=60°,
∴AB∥CD,DE∥CF,
又∵EF∥AB,
∴EF∥CD,
∴四边形EFCD是菱形;
(2)连接DF,与CE相交于点G,
由CD=4,可知CG=2,
∴DG=
 ,
,∴DF=4
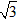 。
。
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
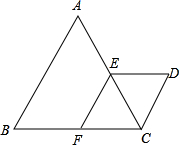 如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB
如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB

