题目内容
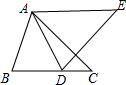如图，D是BC上一点，AB=AD，BC=DE．（1）在条件：①∠C=∠E，②AC=AE中，选择②可得
△ABC≌△ADE
△ABC≌△ADE
．（2）在（1）的条件下，求证：∠CDE=∠BAD．
分析：（1）根据SSS推出三角形全等即可；
（2）根据全等得出∠BAC=∠DAE，求出∠BAD=∠EAC，根据全等三角形性质得出∠E=∠C，根据三角形内角和定理求出∠EAC=∠CDE，即可得出答案．
（2）根据全等得出∠BAC=∠DAE，求出∠BAD=∠EAC，根据全等三角形性质得出∠E=∠C，根据三角形内角和定理求出∠EAC=∠CDE，即可得出答案．
解答：证明：（1）∵在△ABC和△ADE中
∴△ABC≌△ADE，
故答案为：△ABC≌△ADE．
（2）∵△ABC≌△ADE，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠BAD=∠EAC，
∵△ABC≌△ADE，
∴∠E=∠C，
∵∠AOE=∠DOC，∠E+∠AOE+∠EAC=180°，∠C+∠DOC+∠CDE=180°，
∴∠CDE=∠EAC，
∵∠BAD=∠EAC，
∴∠CDE=∠BAD．
|
∴△ABC≌△ADE，
故答案为：△ABC≌△ADE．
（2）∵△ABC≌△ADE，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
∴∠BAD=∠EAC，
∵△ABC≌△ADE，
∴∠E=∠C，
∵∠AOE=∠DOC，∠E+∠AOE+∠EAC=180°，∠C+∠DOC+∠CDE=180°，
∴∠CDE=∠EAC，
∵∠BAD=∠EAC，
∴∠CDE=∠BAD．
点评：本题考查了全等三角形的性质和判定，三角形面积和定理的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
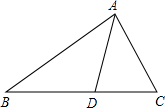已知：如图，D是BC上一点，AD平分∠BAC，AB=3，AC=2，若S△ABD=a，则S△ADC=
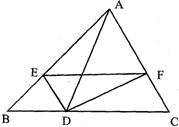26、如图，D是BC上一点，DE平分∠ADB交AB于E，DF⊥DE交AC于F，连接EF．
13、如图，D是BC上一点，E是AB上一点，AD、CE交于点P，且AE：EB=3：2，CP：CE=5：6，那么DB：CD=
如图，E是BC上一点，AB⊥BC，且AB=BC，过B点作BD⊥AE于O点，CD∥AE，在以下两个结论中，选择正确的一个结论，并加以证明．