题目内容
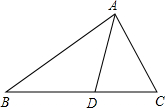 已知:如图,D是BC上一点,AD平分∠BAC,AB=3,AC=2,若S△ABD=a,则S△ADC=
已知:如图,D是BC上一点,AD平分∠BAC,AB=3,AC=2,若S△ABD=a,则S△ADC=分析:过点D分别作DE⊥AB.DF⊥AC.利用角平分线的性质求出DE=
a=DF,然后即可求出S△ADC.
| 2 |
| 3 |
解答: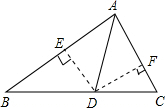 解:如图,过点D分别作DE⊥AB,DF⊥AC.
解:如图,过点D分别作DE⊥AB,DF⊥AC.
∵AD平分∠BAC,
∴DE=DF,
∵若S△ABD=a,即
AB×DE=a,
则DE=
a=DF,
则S△ADC=
×AC×DF=
×2×
a=
a.
故答案为:
a.
 解:如图,过点D分别作DE⊥AB,DF⊥AC.
解:如图,过点D分别作DE⊥AB,DF⊥AC.∵AD平分∠BAC,
∴DE=DF,
∵若S△ABD=a,即
| 1 |
| 2 |
则DE=
| 2 |
| 3 |
则S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题主要考查角平分线的性质这一知识点,解答此题的关键是利用角平分线的性质求出DE=
a,难度不大,属于基础题,要求学生应熟练掌握.
| 2 |
| 3 |

练习册系列答案
相关题目
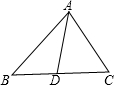 已知:如图,D是BC上一点,AD平分∠BAC,AB=3cm,AC=2cm
已知:如图,D是BC上一点,AD平分∠BAC,AB=3cm,AC=2cm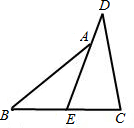 22、阅读下面的题目及分析过程,并按要求进行证明.
22、阅读下面的题目及分析过程,并按要求进行证明.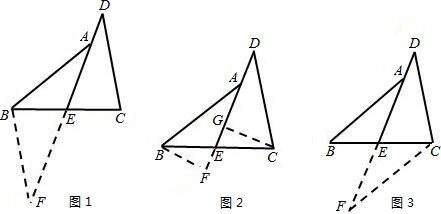
 已知:如图,E是BC的中点,∠1=∠2,AE=DE.AB和DC相等吗?请说明理由.
已知:如图,E是BC的中点,∠1=∠2,AE=DE.AB和DC相等吗?请说明理由. 已知:如图,AD是BC上的中线,且DF=DE.求证:△DBE≌△DCF.
已知:如图,AD是BC上的中线,且DF=DE.求证:△DBE≌△DCF.