题目内容
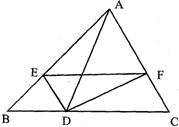26、如图，D是BC上一点，DE平分∠ADB交AB于E，DF⊥DE交AC于F，连接EF．（1）试说明：DF平分∠ADC；
（2）若∠BDE=50°30′，求∠ADC的度数．
分析：（1）利用角平分线的性质可得出∠1=∠2，再由DF⊥DE可得出∠2+∠3=90°，再利用平角的性质即可解答；
（2）根据DE平分∠ADB可求出∠BDA的度数，再根据邻补角的性质即可解答．
（2）根据DE平分∠ADB可求出∠BDA的度数，再根据邻补角的性质即可解答．
解答：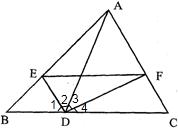
解：（1）∵DE平分∠ADB，∴∠1=∠2，
∵DF⊥DE，∴∠2+∠3=90°，
∵∠1+∠2+∠3+∠4=180°，
∴∠1+∠4=90°，
∴∠3=∠4，
∴DF平分∠ADC．
（2）∵∠1=50°30′，
∴∠BDA=∠2×50°30′=101°，
∴∠ADC=180°-101°=79°．
解：（1）∵DE平分∠ADB，∴∠1=∠2，∵DF⊥DE，∴∠2+∠3=90°，
∵∠1+∠2+∠3+∠4=180°，
∴∠1+∠4=90°，
∴∠3=∠4，
∴DF平分∠ADC．
（2）∵∠1=50°30′，
∴∠BDA=∠2×50°30′=101°，
∴∠ADC=180°-101°=79°．
点评：本题考查的是角平分线的性质及判定，难度一般．
练习册系列答案
阅读快车系列答案
相关题目
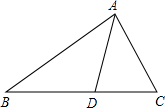已知：如图，D是BC上一点，AD平分∠BAC，AB=3，AC=2，若S△ABD=a，则S△ADC=
13、如图，D是BC上一点，E是AB上一点，AD、CE交于点P，且AE：EB=3：2，CP：CE=5：6，那么DB：CD=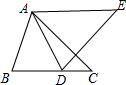
如图，D是BC上一点，AB=AD，BC=DE．
如图，E是BC上一点，AB⊥BC，且AB=BC，过B点作BD⊥AE于O点，CD∥AE，在以下两个结论中，选择正确的一个结论，并加以证明．