题目内容
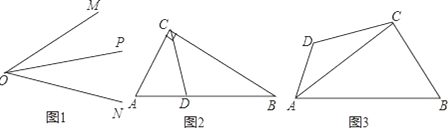
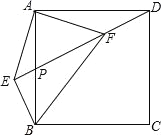
【题目】如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=![]() AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
【答案】D
【解析】
试题分析:根据已知和正方形的性质推出∠EAB=∠DAF,∠EBA=∠ADP,AB=AD,证△ABE≌△ADF即可;取EF的中点M,连接AM,推出AM=MF=EM=DF,证∠AMB=∠FMB,BM=BM,AM=MF,推出△ABM≌△FBM即可;求出∠FDC=∠EBF,推出△BEF≌△DFC即可.
在正方形ABCD中,AB=AD,∠BAD=90°, ∴∠DAF+∠BAF=90°, ∵AF⊥AE,
∴∠BAE+∠BAF=90°, ∴∠BAE=∠DAF, ∵BE⊥DP, ∴∠ABE+∠BPE=90°,
又∵∠ADF+∠APD=90°,∠BPE=∠APD, ∴∠ABE=∠ADF, 在△ABE和△ADF中,
∴△ABE≌△ADF(ASA), ∴AE=AF, ∴△AEF是等腰直角三角形,
∴EF=![]() AF;故①正确; ∴AE=AF,BE=DF, ∴∠AEF=∠AFE=45°,取EF的中点M,连接AM,
AF;故①正确; ∴AE=AF,BE=DF, ∴∠AEF=∠AFE=45°,取EF的中点M,连接AM,
∴AM⊥EF,AM=EM=FM, ∴BE∥AM, ∵AP=BP, ∴AM=BE=DF, ∴∠EMB=∠EBM=45°,
∴∠AMB=90°+45°=135°=∠FMB, 在△ABM和△FBM中, ∴△ABM≌△FBM(SAS),
∴AB=BF,故②正确; ∴∠BAM=∠BFM, ∵∠BEF=90°,AM⊥EF,
∴∠BAM+∠APM=90°,∠EBF+∠EFB=90°, ∴∠APF=∠EBF, ∵AB∥CD, ∴∠APD=∠FDC,
∴∠EBF=∠FDC, 在△BEF和△DFC中, ∴△BEF≌△DFC(SAS),
∴CF=EF,∠DFC=∠FEB=90°, 故④正确; ∴CF⊥DEP, ∵BE⊥DP, ∴CF∥BE;故③正确.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案