题目内容
【题目】阅读探索题:
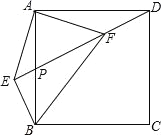
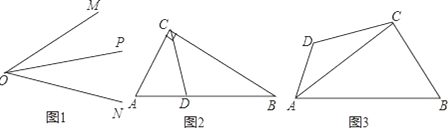
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,在射线OP上任取一点A(O点除外),连接AB,AC,求证:△AOB≌△AOC.
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图2:在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系;
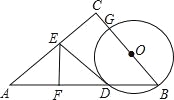
②如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.
【答案】(1)证明见解析;(2)①BC=AC+AD;②21.
【解析】试题分析:(1)根据以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,OP是∠MON的平分线,运用SAS判定△AOB≌△AOC即可;
(2)先截取CE=CA,连接DE,根据SAS判定△CAD≌△CED,得出AD=DE,∠A=∠CED=60°,AC=CE,进而得出结论BC=AC+AD;
(3)先截取AE=AD,连接CE,作CH⊥AB,垂足为点H,根据△ADC≌△AEC,在Rt△ACH和Rt△CEH中,设EH=HB=x,利用CH为公共边,列出方程172-(9+x)2=102-x2,求得x的值即可得到AB的长.
试题解析:(1)如图1,以O为圆心任意长为半径作弧,交射线ON,OM为C,B两点,则OB=OC,

∵OP是∠MON的平分线,
∴∠AOB=∠AOC,
在△AOB和△AOC, ,
,
∴△AOB≌△AOC(SAS);
(2)BC=AC+AD
如图2,截取CE=CA,连接DE,

∵CD平分∠ACB,
∴∠ACD=∠ECD,
在△ACD与△ECD中, ,
,
∴△CAD≌△CED(SAS),
∴AD=DE,∠A=∠CED=60°,AC=CE,
∵∠ACB=90°,∠A=60°,
∴∠B=30°,
∴∠B=∠EDB=30°,
∴DE=EB=AD,
∴BC=AC+AD;
(3)如图,截取AE=AD,连接CE,作CH⊥AB,垂足为点H,

同理△ADC≌△AEC,
∴AE=AD=9,CD=CE=10=CB,
∵CH⊥AB,CE=CB,
∴EH=HB,
设EH=HB=x,
在Rt△ACH和Rt△CEH中
172-(9+x)2=102-x2,
解得:x=6,
∴AB=21.