Question

【题目】已知抛物线y=ax2+bx﹣3经过A（﹣1，0）、B（3，0）两点，与y轴交于C点．

（1）求抛物线的解析式；

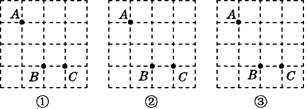
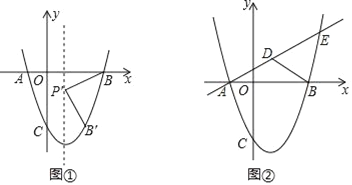
（2）如图①，抛物线的对称轴上有一点P，且点P在x轴下方，线段PB绕点P顺时针旋转90°，点B的对应点B′恰好落在抛物线上，求点P的坐标．

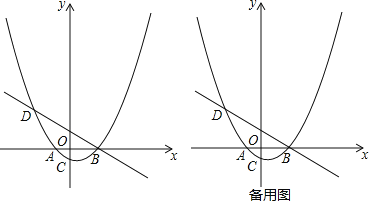
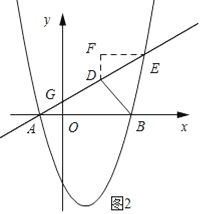
（3）如图②，直线y=x+交抛物线于A、E两点，点D为线段AE上一点，连接BD，有一动点Q从B点出发，沿线段BD以每秒1个单位的速度运动到D，再沿DE以每秒2个单位的速度运动到E，问：是否存在点D，使点Q从点B到E的运动时间最少？若存在，请求出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）a=1，b=﹣2；（2）P（1，﹣1）（3）D（3，）．

【解析】（1）将点A和点B的坐标代入抛物线的解析式可得到关于a、b的方程组，从而可求得a、b的值；

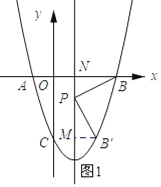
（2）先求得抛物线的对称轴为x=1．过点B′作B′M⊥对称轴，垂足为M．然后证明△BNP≌△PMB，依据全等三角形的性质可知BN=PM=3，PN=MB′．设P（1，m），则点B′的坐标为（1﹣m，m﹣2），最后将点B′的坐标代入抛物线的解析式求解即可；

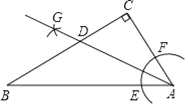
（3）过点E作EF∥x轴，作点DF∥y轴，则∠EFD=90°．先求得点G的坐标，则可得到OG=，在Rt△AGO中，利用特殊锐角三角函数值可求得∠A的度数，则∠FED=30°，依据函数30°直角三角形的性质可得到DF=DE．则动点Q沿DE以每秒2个单位的速度运动到E与它一每秒1个单位的速度运动东F所用时间相等．故此当BD+DF最短时，所用时间最短，依据两点之间线段最短可知当B，D，F在一条直线上时，所用时间最短，此时BE⊥BF，则点D的横坐标为3，然后由函数解析式再求得点D的纵坐标即可．

解：（1）将点A和点B的坐标代入得：，

解得：a=1，b=﹣2．

∴抛物线的解析式为y=x2﹣2x﹣3．

（2）∵A（﹣1，0），B（3，0），

∴抛物线的对称轴为x=1．

如图所示：过点B′作B′M⊥对称轴，垂足为M．

∵∠BPB′=90°，

∴∠BPN+∠B′PM=90°．

∵∠BPN+∠PBN=90°，

∴∠PNB=∠B′PM．

在△BPN和△PB′M中

∠PBN＝∠B′PM，∠BNP＝∠PM B′，PB=PB′，

∴△BNP≌△PMB．

∴BN=PM=3，PN=MB′．

设P（1，m），则点B′的坐标为（1﹣m，m﹣2）．

将点B′的坐标代入抛物线的解析式得：

（1﹣m）2﹣2（1﹣m）﹣3=m﹣2，解得：m1=﹣1，m2=2．

∵点P在x轴的下方，

∴m=﹣1．

∴P（1，﹣1）．

（3）存在．

如图所示：过点E作EF∥x轴，作点DF∥y轴，则∠EFD=90°．

将x=0代入直线AE的解析式得y=，

∴OG=．

∴tan∠GAO=．

∴∠FEA=∠GAO=30°．

∴DF=DE．

∴动点Q沿DE以每秒2个单位的速度运动到E与它一每秒1个单位的速度运动东F所用时间相等．

∴当BD+DF最短时，所用时间最短．

∴当B，D，F在一条直线上时，所用时间最短．

∴点D的横坐标为3．

将x=3代入直线AE的解析式得：y=．

∴D（3，）．

“点睛”本题考查了二次函数图象的基本性质，最值问题及全等三角形性质，三角函数等知识点，对存在性问题进请说明理由难度适中，适合学生巩固知识．