题目内容
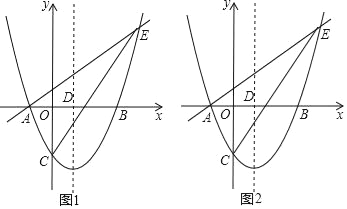
【题目】如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=60°.
(1)求点E到BC的距离;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交BC于M,过M作MN//AB交折线ADC于N,连结PN,设EP=x.
①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN的周长;若改变,请说明理由;
②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.



图1 图2 图3
【答案】(1) ![]() (2)
(2) ![]() +
+![]() +4 当x=2或4或5-
+4 当x=2或4或5-![]() 时,△PMN为等腰三角形
时,△PMN为等腰三角形
【解析】【试题分析】(1)在直角三角形BEG中,利用三角函数求解;(2)①如图4,当点N在线段AD上时,△PMN的形状不发生改变.过点N作NH⊥EF于H,设PH与NM交于点Q.先求PQ、PN、PM,再求出MN,最后求出△PMN的周长即可;②按照当PM=PN时, 当MP=MN时,当NP=NM时, 三种情况分类讨论即可.
【试题解析】
(1)如图4,过点E作EG⊥BC于G.
在Rt△BEG中, ![]() ,∠B=60°,
,∠B=60°,
所以![]() ,
, ![]() .
.
所以点E到BC的距离为![]() .
.
(2)因为AD//EF//BC,E是AB的中点,所以F是DC的中点.
因此EF是梯形ABCD的中位线,EF=4.
①如图4,当点N在线段AD上时,△PMN的形状不发生改变.
过点N作NH⊥EF于H,设PH与NM交于点Q.
在矩形EGMP中,EP=GM=x,PM=EG=![]() .
.
在平行四边形BMQE中,BM=EQ=1+x.
所以BG=PQ=1.
因为PM与NH平行且相等,所以PH与NM互相平分,PH=2PQ=2.
在Rt△PNH中,NH=![]() ,PH=2,所以PN=
,PH=2,所以PN=![]() .
.
在平行四边形ABMN中,MN=AB=4.
因此△PMN的周长为![]() +
+![]() +4.
+4.
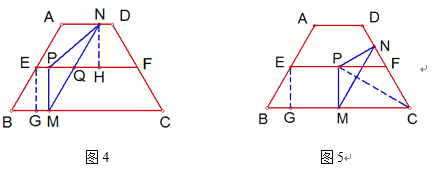
②当点N在线段DC上时,△CMN恒为等边三角形.
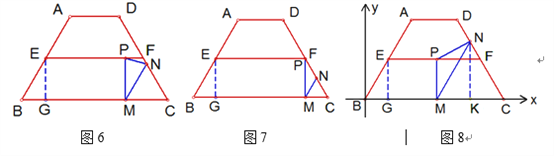
如图5,当PM=PN时,△PMC与△PNC关于直线PC对称,点P在∠DCB的平分线上.
在Rt△PCM中,PM=![]() ,∠PCM=30°,所以MC=3.
,∠PCM=30°,所以MC=3.
此时M、P分别为BC、EF的中点,x=2.
如图6,当MP=MN时,MP=MN=MC=![]() ,x=GM=GC-MC=5-
,x=GM=GC-MC=5-![]() .
.
如图7,当NP=NM时,∠NMP=∠NPM=30°,所以∠PNM=120°.
又因为∠FNM=120°,所以P与F重合.
此时x=4.
综上所述,当x=2或4或5-![]() 时,△PMN为等腰三角形.
时,△PMN为等腰三角形.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】刘明上周末买进某只股票2000股,每股38元,下表为本周内每日该股票的涨跌情况(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +2.1 | +1.5 | -2 | -1 | +3.8 | -2.7 |
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低每股多少元?
(3)已知买进股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交税,刘明周六收盘前全部卖出股票获利多少?