Question

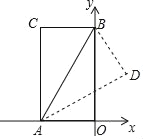
【题目】如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为（0，3），∠ABO=30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为_____．

Answer 1

【答案】(,)

【解析】分析：根据翻折变换的性质和矩形的性质可得∠DAM=30°，AC=OB=AD=3，，结合锐角三角函数关系得出线段AN和DM的长，进而得出D点坐标．

详解：∵四边形AOBC是矩形，∠ABO=30°，点B的坐标为（0，3），

∴AC=OB=3，∠CAB=30°，

∴BC=ACtan30°=3×=3，

∵将△ABC沿AB所在直线对折后，点C落在点D处，

∴∠BAD=30°，AD=3，

过点D作DM⊥x轴于点M，

∵∠CAB=∠BAD=30°，

∴∠DAM=30°，

∴DM=AD=，

∴AM=3×cos30°=，

∴MO=-3=，

∴点D的坐标为（，）．

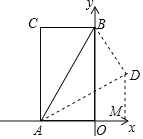
故答案为：（，）．