题目内容
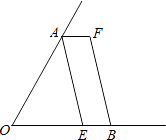
【题目】如图,已知AD是三角形纸片ABC的高,将纸片沿直线EF折叠,使点A与点D重合,给出下列判断: ①EF是△ABC的中位线;
②△DEF的周长等于△ABC周长的一半;
③若四边形AEDF是菱形,则AB=AC;
④若∠BAC是直角,则四边形AEDF是矩形,
其中正确的是( )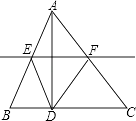
A.①②③
B.①②④
C.②④
D.①③④
【答案】A
【解析】解:∵AD是△ABC的高, ∴AD⊥BC,
∴∠ADC=90°,
根据折叠可得:EF是AD的垂直平分线,
∴AO=DO= ![]() AD,AD⊥EF,
AD,AD⊥EF,
∴∠AOF=90°,
∴∠AOF=∠ADC=90°,
∴EF∥BC,
∴△AEF∽△ABC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴EF是△ABC的中位线,
故①正确;
∵EF是△ABC的中位线,
∴△AEF的周长是△ABC的一半,
根据折叠可得△AEF≌△DEF,
∴△DEF的周长等于△ABC周长的一半,
故②正确;
∵EF是△ABC的中位线,
∴AE= ![]() AB,AF=
AB,AF= ![]() AC,
AC,
若四边形AEDF是菱形,
则AE=AF,
∴AB=AC,
故③正确;
根据折叠只能证明∠BAC=∠EDF=90°,
不能确定∠AED和∠AFD的度数,故④错误;
故选:A.
【考点精析】本题主要考查了三角形中位线定理和菱形的性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.

练习册系列答案
相关题目