题目内容
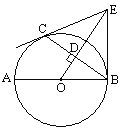
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.
(1)求证:BE与⊙O相切;
(2)连结AD并延长交BE于点F,若OB=6,且sin∠ABC=![]() ,求BF的长.
,求BF的长.
【答案】(1)BE是⊙O的切线,(2)BF=![]() .
.
【解析】试题分析: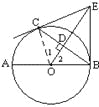
解:(1)连结CO,∵OD⊥BC,∴∠1=∠2,再由CO=OB,OE公共,
∴△OCE≌△OBE(SAS )
∴∠OCE=∠OBE,
又CE是切线,∠OCE=90°,∴∠OBE=90°∴BE与⊙O相切
(2)
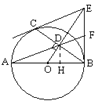
备用图中,作DH⊥OB于H,H为垂足,
∵在Rt△ODB中,OB=6,且sin∠ABC=![]() ,∴OD=4,
,∴OD=4,
同理Rt△ODH∽Rt△ODB,∴DH=![]() ,OH=
,OH=![]()
又∵Rt△ABF∽Rt△AHD,∴FB︰DH=AB︰AH,
∴FB=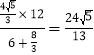
(其他方法同样给分)

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目