题目内容
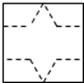如图，将一张边长为6的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，则剩余部分的面积为
- A.36
- B.
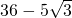
- C.
- D.
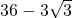
C
分析：首先根据题意求得等边三角形的边长为2，高为
，继而可求得矩形ABCD的高，则可求得矩形ABCD的面积与△EMN、△FPQ的面积，继而求得答案．
解答：
解：∵将一张边长为6的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，
∴AM=MN=BN=
AB=×6=2，
∴△EMN的边长为：2，则高为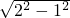
=，
∴AD=6-2，
∴矩形ABCD的面积为：6×（6-2）=36-12，S△FPQ=S△EMN=
×2×=，
∴剩余部分的面积为：36-（36-12）-2=10．
故选C．
点评：此题考查了正方形的性质、矩形的性质、等边三角形的性质以及正三棱柱的知识．此题综合性较强，难度适中，考查了学生的空间想象能力，注意数形结合思想的应用．
分析：首先根据题意求得等边三角形的边长为2，高为
，继而可求得矩形ABCD的高，则可求得矩形ABCD的面积与△EMN、△FPQ的面积，继而求得答案．解答：
解：∵将一张边长为6的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，∴AM=MN=BN=
AB=×6=2，∴△EMN的边长为：2，则高为
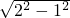=，∴AD=6-2
，∴矩形ABCD的面积为：6×（6-2
）=36-12，S△FPQ=S△EMN=×2×=，∴剩余部分的面积为：36-（36-12
）-2=10．故选C．
点评：此题考查了正方形的性质、矩形的性质、等边三角形的性质以及正三棱柱的知识．此题综合性较强，难度适中，考查了学生的空间想象能力，注意数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
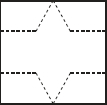如图，将一张边长为3的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，这个棱柱的侧面积为（ ）A、9-3
| ||||
| B、9 | ||||
C、9-
| ||||
D、9-
|
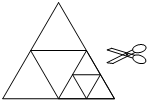如图，将一张边长为4的正三角形纸片剪成四个全等的小正三角形，得到4个小正三角形，然后将其中的一个三角形再剪成四个全等的小正三角形，得到7个小正三角形．根据以上操作，若得到2014个小正三角形时，则最小正三角形的面积等于（ ）A、
| ||||
B、
| ||||
C、（
| ||||
D、
|
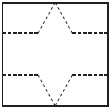如图，将一张边长为3的正方形纸片按虚线裁剪（去掉四个直角梯形）后，恰好围成一个底面是正三角形的棱柱，这个棱柱的侧面积为