题目内容
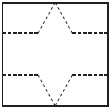 如图,将一张边长为3的正方形纸片按虚线裁剪(去掉四个直角梯形)后,恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为
如图,将一张边长为3的正方形纸片按虚线裁剪(去掉四个直角梯形)后,恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为分析:这个棱柱的侧面展开正好是一个长方形,长为3,宽为3减去两个三角形的高,再用长方形的面积公式计算即可解答.
解答:解:∵将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,
∴这个正三角形的底面边长为1,高为
=
,
∴侧面积为长为3,宽为3-
的长方形,面积为9-3
.
故答案为:9-3
.
∴这个正三角形的底面边长为1,高为
12-(
|
| ||
| 2 |
∴侧面积为长为3,宽为3-
| 3 |
| 3 |
故答案为:9-3
| 3 |
点评:此题主要考查了剪纸问题的实际应用,动手操作拼出图形,并能正确进行计算是解答本题的关键.

练习册系列答案
相关题目
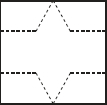 如图,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为( )
如图,将一张边长为3的正方形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为( )A、9-3
| ||||
| B、9 | ||||
C、9-
| ||||
D、9-
|
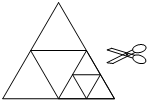 如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2014个小正三角形时,则最小正三角形的面积等于( )
如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2014个小正三角形时,则最小正三角形的面积等于( )A、
| ||||
B、
| ||||
C、(
| ||||
D、
|