题目内容
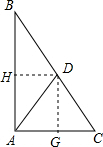
已知在Rt△ABC中，∠A=90°，sinB=
，BC=a，点D在边BC上，将这个三角形沿直线AD折叠，点C恰好落在边AB上，那么BD=______．（用a的代数式表示）
| ||
| 5 |
过D作DH⊥AB于点H，作DG⊥AC于点G．
∵在Rt△ABC中，∠BAC=90°，sinB=
，BC=a，
∴AC=
a，AB=
a，
∵S△ABC=
AB•AC=
，
由折叠的性质可得：AD平分∠CAB，
∴DH=DG，
设DH=x，
∴S△ABC=S△DAC+S△ABD=
AB•DH+
AC•DG=
DH（AB+AC）=
•x•（
a+
a）=
ax，
∴
ax=
，
解得：x=
a，
∴DH=AH=
a，
∴BH=AB-AH=
a，
∴BD=
=
a．
故答案为：
a．
∵在Rt△ABC中，∠BAC=90°，sinB=
| ||
| 5 |
∴AC=
| ||
| 5 |
2
| ||
| 5 |
∵S△ABC=
| 1 |
| 2 |
| a2 |
| 5 |
由折叠的性质可得：AD平分∠CAB，
∴DH=DG，
设DH=x，
∴S△ABC=S△DAC+S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
3
| ||
| 10 |
∴
3
| ||
| 10 |
| a2 |
| 5 |
解得：x=
2
| ||
| 15 |
∴DH=AH=
2
| ||
| 15 |
∴BH=AB-AH=
4
| ||
| 15 |
∴BD=
| DH2+BH2 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
练习册系列答案
相关题目
