题目内容
【题目】等腰三角形ABC内接于圆O,AB=AC,AB的垂直平分线MN与边AB交于点M,与AC所在的直线交于点N,若∠ANM=70°,则劣弧![]() 所对的圆心角的度数为 .
所对的圆心角的度数为 .
【答案】160°或20°.
【解析】
试题分析:此题根据△ABC中∠A为锐角与钝角,分为两种情况解答,由线段垂直平分线的性质与等腰三角形的性质即可求得答案.
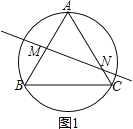
解:当∠A 为锐角时,如图1,
∵MN是AB的垂直平分线,
∴∠AMN=90°,
∵∠ANM=70°,
∴∠A=20°,
∵AB=AC,
∴∠B=80°,
∴劣弧![]() 所对的圆心角的度数为:160°;
所对的圆心角的度数为:160°;
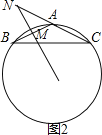
当∠A为钝角时,如图2,
∵MN是AB的垂直平分线,
∴∠AMN=90°,
∵∠ANM=70°,
∴∠BAN=20°,
∴∠BAC=160°,
∵AB=AC,
∴∠B=10°,
∴劣弧![]() 所对的圆心角的度数为:20°,
所对的圆心角的度数为:20°,
故答案为:160°或20°.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目