题目内容
【题目】点P是菱形ABCD的对角线AC上的一个动点，已知AB=1，∠ADC=120°, 点M，N分别是AB，BC边上的中点，则△MPN的周长最小值是______.
【答案】
.
【解析】
先作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值．然后证明四边形ABNM′为平行四边形，即可求出MP+NP=M′N=AB=1，再求出MN的长即可求出答案．
如图，作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值，最小值为M′N的长．
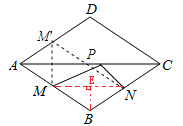
∵菱形ABCD关于AC对称，M是AB边上的中点，
∴M′是AD的中点，
又∵N是BC边上的中点，
∴AM′∥BN，AM′=BN，
∴四边形ABNM′是平行四边形，
∴M′N=AB=1，
∴MP+NP=M′N=1，即MP+NP的最小值为1，
连结MN，过点B作BE⊥MN，垂足为点E，
∴ME=
MN，
在Rt△MBE中，
，BM=
∴ME=
，
∴MN=
∴△MPN的周长最小值是+1.
故答案为：+1.
练习册系列答案
相关题目
【题目】李老师为了了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体情况统计如下：
阅读时间 （小时） | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数（名） | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是（ ）
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
