题目内容
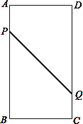
【题目】如图，在矩形ABCD中，AB=16cm，BC=6cm，点P从A出发沿AB以3cm/s的速度向点B移动，一直到达点B为止；同时，点Q从点C出发沿以2cm/s的速度向点D移动．经过多长时间P、Q两点的距离是10？
【答案】P，Q两点从出发经过1.6或4.8秒时，点P，Q间的距离是10cm.
【解析】试题分析：作PH⊥CD，垂足为H，设运动时间为t秒，用t表示线段长，用勾股定理列方程求解．
当P在Q下方时，方法同上，只不过表示等边三角形底边一半的时候稍有不同．
试题解析：设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm，
作PH⊥CD，垂足为H，
则PH=BC=6，PQ=10，HQ=CD﹣AP﹣CQ=16﹣5t．
∵PH2+HQ2=PQ2，
可得：（16﹣5t）2+62=102，
解得t1=4.8，t2=1.6．
答：P，Q两点从出发经过1.6或4.8秒时，点P，Q间的距离是10cm
练习册系列答案
阅读快车系列答案
相关题目
