Question

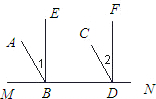
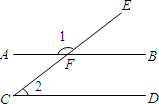
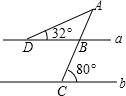
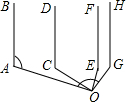
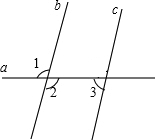
已知AB∥CD，线段EF分别与AB、CD相交于点E、F．

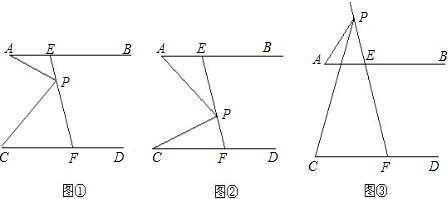
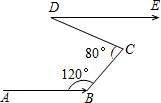
（1）如图①，当∠A=25°，∠APC=70°时，求∠C的度数；
（2）如图②，当点P在线段EF上运动时（不包括E、F两点），∠A、∠APC与∠C之间有什么确定的相等关系？试证明你的结论；
（3）如图③，当点P在线段FE的延长线上运动时，（2）中的结论还成立吗？如果成立，说明理由；如果不成立，试探究它们之间新的相等关系并证明．

Answer 1

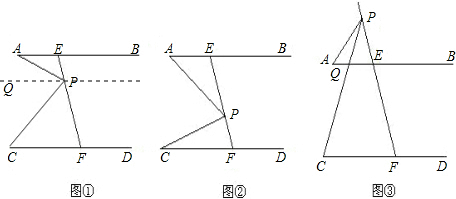
（1）过点P作PQ∥AB，
∴∠APQ=∠A=25°．
∴∠QPC=∠APC-∠APQ=45°．
∵AB∥CD，PQ∥AB，
∴CD∥PQ．
∴∠C=∠QPC=45°．

（2）∠C=∠APC-∠A．
证明如下：过点P作PQ∥AB．
∴∠APQ=∠A．
∴∠QPC=∠APC-∠APQ=∠APC-∠A．
∵AB∥CD，PQ∥AB，
∴CD∥PQ．
∴∠C=∠QPC．
∴∠C=∠APC-∠A．

（3）不成立，新的相等关系为∠C=∠APC+∠A．
证明：设AB与CP相交于Q，则∠PQB=∠APC+∠A．
∵AB∥CD，
∴∠C=∠PQB，
∴∠C=∠APC+∠A．