题目内容
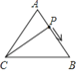
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A观测站在B观测站的正东方向,有一艘小船在点P处,从A处测得小船在北偏西60°方向,从B处测得小船在北偏东45°的方向,点P到点B的距离是3![]() 千米.(注:结果有根号的保留根号)
千米.(注:结果有根号的保留根号)
(1)求A,B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向以![]() 千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.
千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.

【答案】(1)(3+3![]() )千米;(2)3小时.
)千米;(2)3小时.
【解析】试题分析:(1)过点P作PD⊥AB于点D.先解Rt△PBD,得到BD和PD的长,再解Rt△PAD,得到AD和AP的长,然后根据BD+AD=AB,即可求解;
(2)过点B作BF⊥AC于点F.先解Rt△ABF,得出BF和AF的长,再解Rt△BCF,得出CF的长,可求PC=AF+CF-AP,从而求解.
试题解析:(1)如图,过点P作PD⊥AB于点D.

在Rt△PBD中, ![]()
∴BD=PD=3千米.
在Rt△PAD中, ![]()
∴AD= ![]() =
=![]() 千米,PA=6千米.
千米,PA=6千米.
∴AB=BD+AD=![]() (千米);
(千米);
(2)如图,过点B作BF⊥AC于点F.
根据题意得: ![]()
在Rt△ABF中, ![]()
![]() 千米,AF=
千米,AF=![]() AB=
AB=![]() 千米.
千米.
在△ABC中, ![]()
在Rt△BCF中, ![]()
![]() 千米,
千米,
∴PC=AF+CFAP=![]() 千米
千米
故小船沿途考察的时间为: ![]() (小时).
(小时).

 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】呈贡区商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?