题目内容
【题目】如图，四边形ABCD为正方形，边长为4，点F在AB边上，E为射线AD上一点，正方形ABCD沿直线EF折叠，点A落在G处，已知点G恰好在以AB为直径的圆上，则CG的最小值等于（ ）
A.0
B.2 
C.4﹣2
D.2 ﹣2
【答案】D
【解析】解：如图所示：
由翻折的性质可知：AF=FG，AG⊥OE，∠OAE=∠OGE=90°．
∵AF=FG，AG⊥OE，
∴点O是圆半圆的圆心．
∴OG=OA=OB=2．
在△OBC中，由勾股定理可知：OC= 
=2 
．
∵当点O、G、C在一条直线上时，GC有最小值，
∴CG的最小值=OC﹣OG=2 ﹣2．
所以答案是：D．
【考点精析】本题主要考查了线段的基本性质和勾股定理的概念的相关知识点，需要掌握线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |
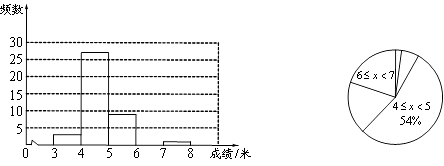
请你结合图表中所提供的信息，回答下列问题：
（1）表中m= ， n=；
（2）请补全频数分布直方图；
（3）在扇形统计图中， 
这一组所占圆心角的度数为度；
（4）如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．
