题目内容
如图,已知二次函数y=x -4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
-4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
(1) y=-x+3;(2) ( ,
,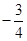 ).
).
解析试题分析:(1)利用y=x2-4x+3的图象交x轴于A、B两点(点A在点B的左侧),抛物线y=x2-4x+3交y轴于点C,即可得出A,B,C点的坐标,将B,C点的坐标分别代入y=kx+b(k≠0),即可得出解析式;
(2)设过D点的直线与直线BC平行,且抛物线只有一个交点时,△BCD的面积最大.
试题解析:(1)设直线BC的解析式为:y=kx+b(k≠0).
令x2-4x+3=0,
解得:x1=1,x2=3,
则A(1,0),B(3,0),C(0,3),
将B(3,0),C(0,3),代入y=kx+b(k≠0),得 ,
,
解得:k=-1,b=3,
BC所在直线为:y=-x+3;
(2)设过D点的直线与直线BC平行,且抛物线只有一个交点时,△BCD的面积最大.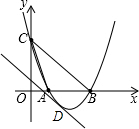
∵直线BC为y=-x+3,
∴设过D点的直线为y=-x+b,
∴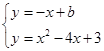 ,
,
∴x2-3x+3-b=0,
∴△=9-4(3-b)=0,
解得b= ,
,
∴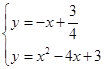 ,
,
解得,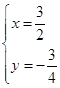 ,
,
则点D的坐标为:( ,
,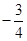 ).
).
考点: 1.抛物线与x轴的交点;2.待定系数法求一次函数解析式;3.二次函数图象上点的坐标特征.

练习册系列答案
相关题目
为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时(包括15吨),采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费,小兰家4、5月份的用水量及收费情况如下表:
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
(2)设每月用水量为n吨,应缴水费为m元,请写出m与n之间的函数关系式.
(3)小兰家6月份的用水量为26吨,则她家要缴水费多少元?
 沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
 与
与 轴相交于点A,与
轴相交于点A,与 轴相交于点B.
轴相交于点B.
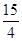 ,试求点P的坐标.
,试求点P的坐标.
 的图象,利用图象:
的图象,利用图象: 的解;
的解; 的解;
的解; ,求
,求 的取值范围。
的取值范围。 的图象与
的图象与 轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.
轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.