题目内容
斜边长为2，两直角边之和为（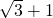
）的直角三角形的面积为
- A.
- B.1
- C.
- D.2（
）
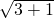A
分析：设斜边为c，两条直角边是a，b．根据已知条件，得
，要求直角三角形的面积，只需利用完全平方公式求
ab的值．
解答：设斜边为c，两条直角边是a，b．
根据题意，得
，
则ab=
[（a+b）2-（a2+b2）]=（4+2-4）=．
故选A．
点评：此题能够根据已知条件得到关于a，b的方程，利用完全平方公式，求得两条直角边的乘积的一半即可．
分析：设斜边为c，两条直角边是a，b．根据已知条件，得
，要求直角三角形的面积，只需利用完全平方公式求ab的值．解答：设斜边为c，两条直角边是a，b．
根据题意，得
，则
ab=[（a+b）2-（a2+b2）]=（4+2-4）=．故选A．
点评：此题能够根据已知条件得到关于a，b的方程，利用完全平方公式，求得两条直角边的乘积的一半即可．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
斜边长为2，两直角边之和为（
+1）的直角三角形的面积为（ ）
| 3 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、2（
|
已知，在△ABC中，∠C=90°，斜边长为7
，两直角边的长分别是关于x的方程x2-3(m+
)x+9m=0
的两个根，则△ABC的内切圆面积是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
的两个根，则△ABC的内切圆面积是（ ）
| A、4π | ||
B、
| ||
C、
| ||
D、
|