题目内容
【题目】在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y= 
的一个交点为P（2，m），与x轴、y轴分别交于点A，B．
（1）求m的值；
（2）若S△AOP=2S△AOB ， 求k的值．
【答案】
（1）解：∵点P（2，m）在双曲线y= 
上，
∴m=4；
（2）解：如图，
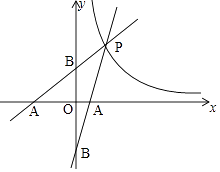
∵S△AOP=2S△AOB，
∴ 
AO|Py|=2× BOOA，
则OB=2，
∴点B的坐标为（0，2）或（0，﹣2），
当B的坐标为（0，2）时，
将点B（0，2）、P（2，4）代入y=kx+b，得：
，
解得：k=1；
当点B的坐标为（0，﹣2）时，
将点B（0，﹣2）、P（2，4）代入y=kx+b，得：
，
解得：k=3；
综上，k的值为1或3．
【解析】（1）将点P坐标代入反比例函数解析式即可求得m的值；（2）由S△AOP=2S△AOB知 
AO|Py|=2× BOOA，据此得出OB的值，即知点B的坐标，待定系数法求解可得k的值．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
