题目内容
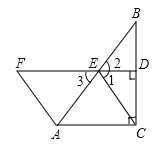
【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

【答案】答案见解析
【解析】试题分析:要证明四边形ACEF是平行四边形,需求证CE∥AF,由已知易得△BEC,△AEF是等腰三角形,则∠1=∠2,∠3=∠F,又∠2=∠3,得到∠1=∠F,故CE∥AF,由此即可得到结论.
试题解析:证明:∵点E为AB中点,∴AE=EB.又∵∠ACB=90°,∴CE=AE=EB.又∵AF=CE,∴AF=AE,∴∠3=∠F.又∵EB=EC,ED⊥BC,∴∠1=∠2(三线合一).又∵∠2=∠3,∴∠1=∠F,∴CE∥AF,∴四边形ACEF是平行四边形.

练习册系列答案
相关题目
【题目】如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
点 | 坐标 | 所在象限或坐标轴 |
A | ||
B | ||
C | ||
D | ||
E | ||
F |

(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;
(4)观察图形,说出(3)中的关系在第三象限中是否存在?