题目内容
已知直角三角形的两直角边分别为6，8，则斜边上的高等于
- A.4
- B.4.8
- C.5
- D.10
B
分析：根据勾股定理求出斜边的长，再根据面积法求出斜边上的高．
解答：设斜边长为c，斜边上的高为h．
由勾股定理可得：c2=62+82，
则c=10，
直角三角形面积S=
×6×8=×10×h，
解得h=4.8．
故选B．
点评：本题考查了利用勾股定理求直角三角形的边长及利用面积法求直角三角形的高，是解此类题目常用的方法．
分析：根据勾股定理求出斜边的长，再根据面积法求出斜边上的高．
解答：设斜边长为c，斜边上的高为h．
由勾股定理可得：c2=62+82，
则c=10，
直角三角形面积S=
×6×8=×10×h，解得h=4.8．
故选B．
点评：本题考查了利用勾股定理求直角三角形的边长及利用面积法求直角三角形的高，是解此类题目常用的方法．
练习册系列答案
相关题目
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=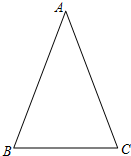
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
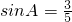，其中A为锐角，试求sadA的值；