题目内容
【题目】如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( ) 
A.BD<2
B.BD=2
C.BD>2
D.以上情况均有可能
【答案】A
【解析】证明:∵AE=AB, ∴∠ABE=∠AEB,同理∠CBD=∠CDB
∵∠ABC=2∠DBE,
∴∠ABE+∠CBD=∠DBE,
∵∠ABE=∠AEB,∠CBD=∠CDB,
∴∠AEB+∠CDB=∠DBE,
∴∠AED+∠CDE=180°,
∴AE//CD,
∵AE=CD,
∴四边形AEDC为平行四边形.
∴DE=AC=AB=BC.
∴△ABC是等边三角形,
∴BC=CD=1,
在△BCD中,∵BD<BC+CD,
∴BD<2.
故选A.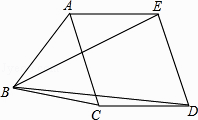
【考点精析】认真审题,首先需要了解平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

