题目内容
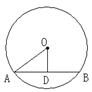
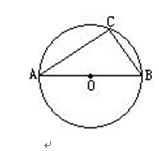
(1)已知:如图1,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE=DF.
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是弧AB的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.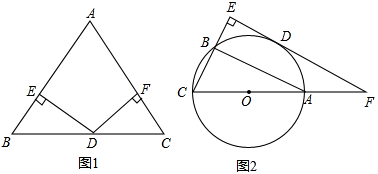
(2)如图2,已知△ABC内接于⊙O,AC是⊙O的直径,D是弧AB的中点,过点D作直线BC的垂线,分别交CB,CA的延长线于E,F,求证:EF是⊙O的切线.

(1)见解析(2)见解析
(1)连接AD,根据等腰三角形的三线合一定理得出AD平分∠BAC,根据角平分线性质得出DE=DF即可;
(2)连接OD,根据圆周角定理得出BA⊥BC,推出EF∥AB,根据垂径定理得出OD⊥AB,即可得出OD⊥EF,根据切线的判定推出即可.
(2)连接OD,根据圆周角定理得出BA⊥BC,推出EF∥AB,根据垂径定理得出OD⊥AB,即可得出OD⊥EF,根据切线的判定推出即可.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
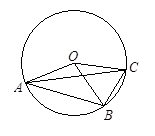
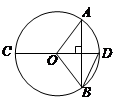
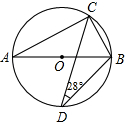

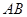 和
和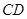 相交于点
相交于点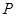 ,
,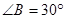 ,
,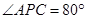 ,则
,则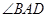 的度数为( )
的度数为( )