题目内容
【题目】如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.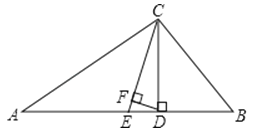
【答案】解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣(∠A+∠B),
=180°﹣(30°+62°),
=180°﹣92°,
=88°,
∵CE平分∠ACB,
∴∠ECB=![]() ∠ACB=44°,
∠ACB=44°,
∵CD⊥AB于D,
∴∠CDB=90°,
∴∠BCD=90°﹣∠B=90°﹣62°=28°,
∴∠ECD=∠ECB﹣∠BCD=44°﹣28°=16°,
∵DF⊥CE于F,
∴∠CFD=90°,
∴∠CDF=90°﹣∠ECD=90°﹣16°=74°.
【解析】首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角的平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
【考点精析】本题主要考查了三角形三边关系的相关知识点,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.

练习册系列答案
相关题目