题目内容
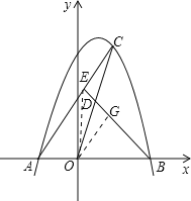
【题目】如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A、B不重合),D是OC的中点,连接BD并延长,交AC于点E.
(1)用含m的代数式表示点A、B的坐标;
(2)求证:![]() ;
;
(3)若点C、点A到y轴的距离相等,且s△CDE=1.6时,求抛物线和直线BE的解析式.
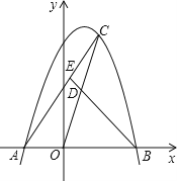
【答案】(1)A(-m,0),b(2m,0);(2)见解析;(3)y=-x2+2x+8,![]()
【解析】
(1)解x的方程-x2+mx+2m2=0,x1=-m,x2=2m.因为点A在点B的左边,且m>0,所以A(-m,0),b(2m,0);
(2)过点O作OG//AC交BE于点G.则△CED∽△OGD,所以![]() ; 由△BOG∽△BAE,得
; 由△BOG∽△BAE,得![]() .因为OB=2m,AB=3m,代入可求出结论;
.因为OB=2m,AB=3m,代入可求出结论;
(3)连接OE,易得S△OCE=2S△CED,因为![]() ,所以
,所以![]() ,即S△AOC=5S△CED=8,点C(m,2m2),由S△AOC=
,即S△AOC=5S△CED=8,点C(m,2m2),由S△AOC=![]() OA|yC|=
OA|yC|=![]() 求得m=2.进而可求出抛物线的解析式和直线BE的解析式.
求得m=2.进而可求出抛物线的解析式和直线BE的解析式.
解:(1)∵抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,
∴关于x的方程-x2+mx+2m2=0有两个不相等的实数根x1和x2;
解得x1=-m,x2=2m.
∵点A在点B的左边,且m>0,
∴A(-m,0),b(2m,0);
(2)过点O作OG∥AC交BE于点G.
∴△CED∽△OGD,∴![]() ;
;
∵DC=DO,
∴CE=OG;
∵OG//AC,
∴△BOG∽△BAE,∴![]() .
.
∵OB=2m,AB=3m,
∴![]() .
.
(3)连接OE.
∵D是OC的中点,
∴S△OCE=2S△CED,
∵![]() ,∴
,∴![]() ,∴S△AOC=5S△CED=8,
,∴S△AOC=5S△CED=8,
∵点C、点A到y轴的距离相等,点C在抛物线y=-x2+mx+2m2上,
∴点C(m,2m2),
∵S△AOC=![]() OA|yC|=
OA|yC|= ![]() =
=![]() ,
,
∴m3=8,解得m=2.
∴抛物线的解析式为y=-x2+2x+8,
∴点B(4,0),点C(2,8).
∴此时D为(1,4),
设直线BE的解析式为:y=kx+b,
∴![]() ,
,
解得
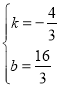 ,
,
∴直线BE的解析式为:![]() .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】某小型加工厂准备每天生产甲、乙两种类型的产品共1000件,原料成本、销售单价,及工人计件工资如表:
甲(元/件) | 乙(元/件) | |
原料成本 | 10 | 8 |
销售单价 | 20 | 16 |
计件工资 | 2 | 1.5 |
设该加工厂每天生产甲型产品x件,每天获得总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若该工厂每天投人总成本不超过10750元,怎样安排甲、乙两种类型的生产量,可使该厂每天所获得的利润最大?并求出最大利润.(总成本=原料成本+计件工资,利润=销售收入一投人总成本)