题目内容
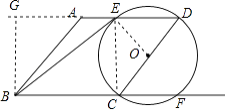
【题目】如图,在菱形ABCD中,AB=4,取CD中点O,以O为圆心OD为半径作圆交AD于E,交BC的延长线交于点F, 
(1)若cos∠AEB= ![]() ,则菱形ABCD的面积为;
,则菱形ABCD的面积为;
(2)当BE与⊙O相切时,AE的长为 .
【答案】
(1)8 ![]()
(2)6﹣2 ![]()
【解析】解:(1.)作BG⊥AD于G,连接CE,
∵四边形ABCD是菱形∴AB=AD=BC=CD=4,AD∥BC,∵CD是直径,∴∠CED=90°,∴CE⊥AD,∴BG∥CE,∴四边形BCEG是矩形,∴GE=BC=4,∵cos∠AEB= ![]() ,∴
,∴ ![]() =
= ![]() ,∴BE=
,∴BE= ![]() ×4=6,∴BG=
×4=6,∴BG= ![]() =
= ![]() =2
=2 ![]() ,∴菱形ABCD的面积=ADBG=4×2
,∴菱形ABCD的面积=ADBG=4×2 ![]() =8
=8 ![]() ;
;
所以答案是8 ![]() ;
;
(2.)连接OE,∵BE与⊙O相切,∴FE⊥BE,∴∠BEG=∠CEO,∵OE=OC,∴∠DCE=∠CEO,∴∠ECD=∠GEB,∴ ![]() =
= ![]() ,∵GE=AD,∴AG=ED,设BG=CE=a,∴
,∵GE=AD,∴AG=ED,设BG=CE=a,∴ ![]() =
= ![]() ,∴16﹣a2=4AE,∴AG2=4AE,即(4﹣AE)2=4AE,∴AE2﹣12AE+16=0,解得AE=6﹣2
,∴16﹣a2=4AE,∴AG2=4AE,即(4﹣AE)2=4AE,∴AE2﹣12AE+16=0,解得AE=6﹣2 ![]() 或AE=6+2
或AE=6+2 ![]() (不合题意,舍去),所以答案是6﹣2
(不合题意,舍去),所以答案是6﹣2 ![]() .
.
【考点精析】利用菱形的性质和切线的性质定理对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目



