��Ŀ����
.(����12��)
��֪������y=ax2+bx+c����P��![]() ��3����E��
��3����E��![]() ��0����ԭ��O��0��0��
��0����ԭ��O��0��0��

��1���������ߵĽ���ʽ��
��2����P����ƽ����x���ֱ��PC��y����C�㣬�������߶Գ����Ҳ�
��λ��ֱ��PC�·����������ϣ���ȡһ��Q������Q��ֱ��QAƽ����y
�ύx����A�㣬��ֱ��PC��B�㣬ֱ��QA��ֱ��PC����������Χ�ɾ���OABC����ͼ�����Ƿ���ڵ�Q��ʹ�á�OPC���PQB���ƣ������ڣ����Q������ꣻ�������ڣ���˵�����ɣ�
��3��������ϣ�2���е�Q����x����Ϸ�������OQ������OABC�ڵ��ĸ������Ρ�OPC����PQB����OQP����OQA֮����������Ĺ�ϵ��Ϊʲô��
�⣺��1������֪�ɵã�
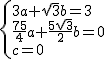
��֮�ã�a=-![]() ��b=
��b=![]() ��c=0��
��c=0��
����ã������ߵĽ���ʽΪ��y=-![]() x2+
x2+![]() x��
x��
��2�����ڣ�
��Q���������m��n������
Ҫʹ��OCP�ס�PBQ��
��������![]()
��֮�ã�m1=3![]() ��m2=
��m2=![]() ��
��
��m1=![]() ʱ��n=2����ΪP�㣬
ʱ��n=2����ΪP�㣬
���Ե�Q��2![]() ��2��
��2��
Ҫʹ��OCP�ס�QPB�����У�![]() ��
��![]()
��֮�ã�m1=3![]() ��m2=
��m2=![]() ��
��
��m=![]() ʱ����ΪP�㣬
ʱ����ΪP�㣬
��m1=3![]() ʱ��n=-3��
ʱ��n=-3��
���Ե�Q��3![]() ��-3����
��-3����
�ʴ�������Q��ʹ�á�OCP���PBQ���ƣ�Q�������Ϊ��2![]() ��2������3
��2������3![]() ��-3����
��-3����
��3����Rt��OCP��
��Ϊtan��COP=![]()
���ԡ�COP=30�ȣ�
��Q�������Ϊ��2![]() ��2��ʱ����BPQ=��COP=30�ȣ�
��2��ʱ����BPQ=��COP=30�ȣ�
���ԡ�OPQ=��OCP=��B=��QAO=90�ȣ�
��ˣ���OPC����PQB����OPQ����OAQ����ֱ�������Σ�
����Rt��OAQ��
��Ϊtan��QOA=![]() ��
��
���ԡ�QOA=30�ȣ�
���С�POQ=��QOA=��QPB=��COP=30�ȣ�
���ԡ�OPC�ס�PQB�ס�OQP�ס�OQA��
����ΪQP��OP��QA��OA��POQ=��AOQ=30�㣬
���ԡ�OQA�ա�OQP��
����:�����Ƕ��κ������ۺ��⣬֪ʶ��϶࣬��һ���Ѷȡ�


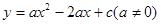 ��ͼ����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��ͼ����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.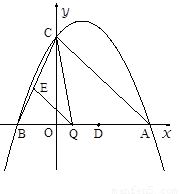
 ��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ��
��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ��