题目内容
如图,⊙H与x轴交于A、B两点,与y轴交于C、D两点,圆心H的坐标是(1,-1 ),半径是
),半径是
.
(1)求经过点D的切线的解析式;
(2)问过点A的切线与过点D的切线是否垂直?若垂直,请写出证明过程;若不垂直,请说明理由.
 ),半径是
),半径是| 5 |
(1)求经过点D的切线的解析式;
(2)问过点A的切线与过点D的切线是否垂直?若垂直,请写出证明过程;若不垂直,请说明理由.
(1)设过点D的切线交x轴于点E,EA=x,
则DE2=EA•EB=x(x+4);
又在Rt△DOE中,DE2=EO2+DO2=(x+1)2+32,
∴(x+1)2+32=x(x+4);(6分)
解得x=5,即EA=5,
点E的坐标为(-6,0);(7分)
设所求切线的解析式为y=kx+b,因为它经过(0,-3)和(-6,0)两点,
则
解得
∴所求解析式为y=-
x-3;(8分)
(2)过点A的切线与过点D的切线互相垂直,证明如下:(9分)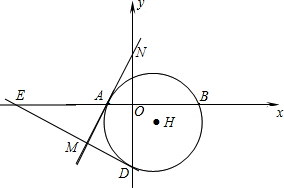
证明:设过点A的切线与DE相交于点M,与y轴相交于点N;
∵AB=CD=4,即有
=
∴∠NAO=∠MDO;(10分)
又∵∠NAO+∠ANO=90°,
∴∠MND+∠MDN=90°;
∴过点A的切线与过点D的切线互相垂直.

则DE2=EA•EB=x(x+4);
又在Rt△DOE中,DE2=EO2+DO2=(x+1)2+32,
∴(x+1)2+32=x(x+4);(6分)
解得x=5,即EA=5,
点E的坐标为(-6,0);(7分)
设所求切线的解析式为y=kx+b,因为它经过(0,-3)和(-6,0)两点,
则
|
解得
|
∴所求解析式为y=-
| 1 |
| 2 |
(2)过点A的切线与过点D的切线互相垂直,证明如下:(9分)

证明:设过点A的切线与DE相交于点M,与y轴相交于点N;
∵AB=CD=4,即有
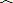 |
| AB |
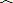 |
| CD |
∴∠NAO=∠MDO;(10分)
又∵∠NAO+∠ANO=90°,
∴∠MND+∠MDN=90°;
∴过点A的切线与过点D的切线互相垂直.


练习册系列答案
相关题目
 图所示.当每天售出的早餐超过150份时,需要增加一名工人.
图所示.当每天售出的早餐超过150份时,需要增加一名工人.