题目内容
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB.如果点P在直线y=x+1上,且点P到直线AB的距离大于或等于1,那么称点P是线段AB的“疏远点”.
(1)判断点C(
,
)是否是线段AB的“疏远点”,并说明理由;
(2)若点Q(m,n)是线段AB的“疏远点”,求m的取值范围.
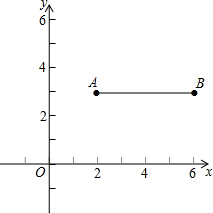
(1)判断点C(
| 5 |
| 2 |
| 7 |
| 2 |
(2)若点Q(m,n)是线段AB的“疏远点”,求m的取值范围.
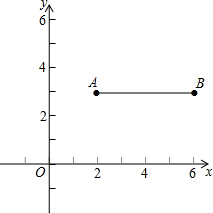
(1)点C(
,
)不是线段AB的“疏远点”.理由如下:
∵
+1=
,
∴点C(
,
)在直线y=x+1上;
∵点A的纵坐标与点B的纵坐标相同,
∴AB∥轴,
∴点C(
,
)到线段AB的距离是
-3=
<1,
∴点C(
,
)不是线段AB的“疏远点”;
(2)∵点Q(m,n)是线段AB的“疏远点”,
∴点Q(m,n)在直线y=x+1上,
∴n=m+1.
①当n=m+1≥3,即m≥2时,
∵AB∥x轴,∴点Q(m,n)到线段AB的距离是n-3,
∴m+1-3≥1,解得m≥3;
②当n=m+1<3,即m<2时,
∵AB∥x轴,∴点Q(m,n)到线段AB的距离是3-n,
∴3-m-1≥1,解得m≤1,
综上所述,m≥3或m≤1.
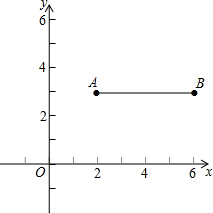
| 5 |
| 2 |
| 7 |
| 2 |
∵
| 5 |
| 2 |
| 7 |
| 2 |
∴点C(
| 5 |
| 2 |
| 7 |
| 2 |
∵点A的纵坐标与点B的纵坐标相同,
∴AB∥轴,
∴点C(
| 5 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
∴点C(
| 5 |
| 2 |
| 7 |
| 2 |
(2)∵点Q(m,n)是线段AB的“疏远点”,
∴点Q(m,n)在直线y=x+1上,
∴n=m+1.
①当n=m+1≥3,即m≥2时,
∵AB∥x轴,∴点Q(m,n)到线段AB的距离是n-3,
∴m+1-3≥1,解得m≥3;
②当n=m+1<3,即m<2时,
∵AB∥x轴,∴点Q(m,n)到线段AB的距离是3-n,
∴3-m-1≥1,解得m≤1,
综上所述,m≥3或m≤1.
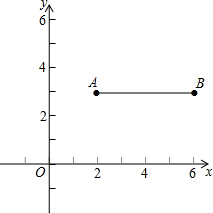

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 、D、E、F为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
、D、E、F为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.

 ),半径是
),半径是